Formal Languages and Translators

Internal

• Programming

TODO Deplete Parsing

Overview

Compiler

Interpreter

Syntax Analysis (Parsing)

The process of building a parse tree from a given string of terminals is called parsing the string.

Grammar

A context-free grammar is a formal specification of a language and has four components:

1. A set of terminal symbols, or terminals, which are the elementary symbols of the language defined by the grammar and they are sometimes referred to as tokens.
2. A set of nonterminals, where each nonterminal represents a set of string of terminals. Nonterminals are sometimes called syntactic variables.
3. A set of productions, where each production consists of a nonterminal called production head or left side of the production, an arrow and a sequence of terminals and/or nonterminals, called the body or the right side of the production. The intuitive intent of a production is to specify one of the written form of a construct - if the head nonterminal represents a construct, then the body represents the written form of the construct. More than one productions may correspond to a specific nonterminal.
4. A start symbol, designated from nonterminals.

Left-Recursive Grammar

Relationship to top-down parsers.

Derivation

The derivation is the process of producing a string of terminals using a grammar, beginning with the start symbol and successively replacing nonterminals with their associated productions, until no nonterminals are left. A string of the language is generated or derived from the start symbol of the grammar.

The derivation process is recursive, as nonterminals get replaced with other sequences of nonterminals and terminals, as defined by the grammar's productions. During the process of derivation, there are two kinds of decisions that can be made:

1. Order in which to replace nonterminals in a production, in case the production body contains more than one nonterminals. The leftmost derivation. The rightmost derivation.

2. Which production to pick, in case there are more than one productions associated with a specific nonterminal.

Language

The terminal strings that can be derived from, or generated by the start symbol of the grammar from the language defined by the grammar. Conversely, a string of the language defined by the grammar is any terminal string that can be derived from the start symbol of the grammar. Another definition of a language generated by a grammar is the set of strings that can generated by some parse tree.

ε

Parse Tree

A parse tree is a graphical representation of how the start symbol of a grammar derives a string in the language defined by the grammar.

The root of the parse tree is labeled by the start symbol. Each interior node of a parse tree represents the application of a production and it is labeled with the name of the nonterminal that is the head of the production. The children node are labeled, from left to right, by the symbols in the body of the production. While is being constructed, the leaves of a parse tree may represent terminals and nonterminals, which at any moment, if they are read from left to right, they constitute the yield or the frontier of the tree, and it is also referred to as a sentential from of the grammar. After a string in the language defined by the grammar is fully parsed, each leaf is labeled by a terminal or by ε.

A parse tree does not contain the information that reflects the order in which productions are applied to replace nonterminals. It is customary to produce parse trees by always producing the leftmost (or rightmost) derivation. Each parse tree has associated with it a unique leftmost and an unique rightmost derivation.

Parse trees are sometimes called concrete syntax trees.

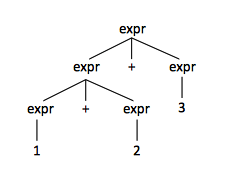
For the following grammar:

expr → expr + expr | NUMBER

and the string "1+2+3", the parse tree is:

(Abstract) Syntax Tree

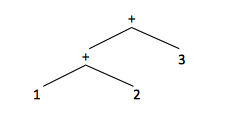
The abstract syntax tree, also referred to as syntax tree, represents the hierarchical syntactic structure of the parsed content, by depicting significant programming constructs. For example, in case of an expression that involves an operator, the fragment of the syntax tree that represents the expression has a node that represents the operator, and its children represent the operands. In general, any programming construct can be handled by marking up an operator for the construct and treating the semantically meaningful components of that construct as operands.

A syntax tree resembles a parse tree to a certain extent. The difference is that for a syntax tree, the internal nodes represent programming constructs, while for parse tree, the internal nodes represent nonterminals. Many nonterminals of a grammar represent programming constructs, but others are intermediate "helpers" of some sort, for example representing terms, factors or other variations of expressions. Examples of productions that are not represented in a syntax tree are expr → term or ε-productions rest → ε. These helpers are dropped into a syntax three. That is why sometimes a parse tree is called a concrete syntax tree.

The corresponding syntax tree of the parse tree represented above is:

Ambiguous Grammars

A grammar that has more than one parse tree generated from a given string is said to be an ambiguous grammar. A string with more than more than one parse tree has usually more than one meaning, we need to design unambiguous grammars, or to use additional rules to resolve the ambiguity.

Parser

Top-Down Parser

A top-down parser is a parser that employs a strategy where it first looks at the highest level of the parse tree and works down the parser tree by using the rewriting rules of the formal grammar. The top-down parser discovers the parse tree starting from the top and incrementally works its way first downwards and then rightwards. Unlike a bottom-up parser, the top-down parser eagerly decides what a construct is much earlier, when it has only scanned the leftmost symbol of that construct and has not yet parsed any of its parts.

If a language grammar has multiple rules that may start with the same leftmost symbols but have different endings, that grammar can be efficiently handled by a deterministic bottom-up parser, but cannot be handled top-down without guesswork and backtracking - so bottom-up parsers handle a somewhat larger range of computer language grammars than top-down parsers.

A recursive descent parsers is a top-down parser build from a set of possibly mutually recursive procedures, where each such procedure usually implements one of the productions of the grammar. In consequence, the structure of the resulting program closely mirrors that of the grammar it recognizes. A predictive recursive descent parser is a recursive descent parser that does not require backtracking, it is called a predictive parser.