LRU Cache: Difference between revisions
| Line 5: | Line 5: | ||
=Overview= | =Overview= | ||
The Least Recently Used caches are justified by the [[The_Optimal_Caching_Problem#The_B.C3.A9l.C3.A1dy_Theorem|Bélády Theorem]] | The Least Recently Used caches are justified by the [[The_Optimal_Caching_Problem#The_B.C3.A9l.C3.A1dy_Theorem|Bélády Theorem]] and it works as follows: the algorithm looks in the past and assumes that what was requested recently will also be requested soon, and what has not been requested for a long time, will continue to not be requested. In consequence, we want recent elements to stay in the cache, and we evict the element that was requested least recently. If this behavior predicts the data behavior, it is says that the data has "locality of reference". | ||
=Implementation= | |||
An implementation where get() is O(1) and put() is O(n): [https://github.com/NovaOrdis/playground/blob/master/leetcode/146-lru-cache/src/main/java/playground/leetcode/lruCache/LRUCacheOn.java Playground LRUCache O(n)] | An implementation where get() is O(1) and put() is O(n): [https://github.com/NovaOrdis/playground/blob/master/leetcode/146-lru-cache/src/main/java/playground/leetcode/lruCache/LRUCacheOn.java Playground LRUCache O(n)] | ||
Latest revision as of 19:44, 20 October 2021
Internal
Overview
The Least Recently Used caches are justified by the Bélády Theorem and it works as follows: the algorithm looks in the past and assumes that what was requested recently will also be requested soon, and what has not been requested for a long time, will continue to not be requested. In consequence, we want recent elements to stay in the cache, and we evict the element that was requested least recently. If this behavior predicts the data behavior, it is says that the data has "locality of reference".
Implementation
An implementation where get() is O(1) and put() is O(n): Playground LRUCache O(n)
An implementation where both get() and put() are O(1): Playground LRUCache O(1)
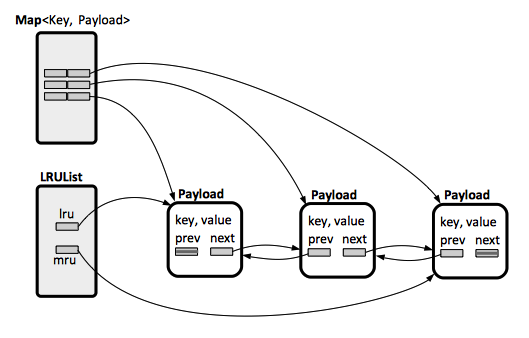
The idea is to maintain the keys in a map (O(1)) for retrieval, but the time ordering is maintained implicitly in the structure of a double-linked list that can be manipulated in O(1): Playground LRUList