Formal Languages and Translators: Difference between revisions
No edit summary |
|||
| (90 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
=External= | |||
* https://medium.com/@mikhail.barash.mikbar/grammars-for-programming-languages-fae3a72a22c6 | |||
=Internal= | =Internal= | ||
* [[ | * [[Programming_Languages_Concepts#Formal_Languages_and_Translators|Programming Languages Concepts]] | ||
<center><font color=darkgray size='+2'>TODO Deplete [[Parsing]]</font></center> | <center><font color=darkgray size='+2'>TODO Deplete [[Parsing]]</font></center> | ||
| Line 10: | Line 12: | ||
<span id='Interpreter'></span>'''Interpreter''' | <span id='Interpreter'></span>'''Interpreter''' | ||
=Programming Language Elements= | |||
==Variable== | |||
==Identifier== | |||
==Statement== | |||
==Expression== | |||
=Lexical Analysis= | =Lexical Analysis= | ||
| Line 17: | Line 29: | ||
==Finite Automata== | ==Finite Automata== | ||
=<span id='Syntax_Analysis | ==Token== | ||
=<span id='Syntax_Analysis'></span>Syntax Analysis (Parsing)= | |||
==Grammar== | ==Grammar== | ||
A context-free grammar is a formal specification of a [[#Language|language]] and has four components: | |||
<span id=' | # <span id='Terminal'></span>A set of '''terminal symbols''', or '''terminals''', which are the elementary symbols of the [[#Language|language]] defined by the grammar and they are sometimes referred to as [[#Token|tokens]]. Technically, a terminal and the ''token name'' are synonymous. | ||
# <span id='Nonterminal'></span>A set of '''nonterminals''', where each nonterminal represents a set of string of terminals. Nonterminals are sometimes called '''syntactic variables'''. Nonterminals impose a hierarchical structure on the language that is key to syntax analysis. | |||
# <span id='Production'></span>A set of '''productions''', where each production consists of a nonterminal called <span id='Production_Head'></span>'''production head''' or '''left side''' of the production, an arrow (→ or ::=) and a sequence of terminals and/or nonterminals, called the <span id='Production_Body'></span>'''body''' or the '''right side''' of the production. The components of the body describe one way in which strings of the nonterminal at the head can be constructed. The intuitive intent of a production is to specify one of the written form of a construct - if the head nonterminal represents a construct, then the body represents the written form of the construct. More than one productions may correspond to a specific nonterminal. A production whose right side consists in a single nonterminal is called a '''single production'''. | |||
# <span id='Start_Symbol'></span>A '''start symbol''', designated from nonterminals. Conventionally, the production for the start symbol are listed first when the grammar is specified. | |||
<span id=' | One of the possible terminals is <span id='empty'></span>'''ε''', which signifies the "empty string". | ||
===Left-Recursive Grammar=== | |||
Relationship to [[#Top-Down_Parser|top-down parsers]]. | |||
===Backus-Naur Form (BNF)=== | |||
===Extended Backus-Naur Form (EBNF)=== | |||
==Derivation and Parsing== | |||
=== | '''<span id='Derivation'></span>Derivation''' is the process of producing a string of terminals using a [[#Grammar|grammar]], beginning with the [[#Start_Symbol|start symbol]] and successively replacing [[#Nonterminals|nonterminals]] with their associated [[#Production|productions]], until no nonterminals are left. The process can also be thought as building of a [[#Parse_Tree|parse tree]], starting from the grammar rules and advancing towards a tree whose all leafs are terminals, where each internal node of the tree corresponds to a head nonterminal whose production is being processed. A string of the language is '''generated''' or '''derived''' from the start symbol of the grammar. | ||
The derivation process is recursive, as nonterminals get replaced with other sequences of nonterminals and terminals, as defined by the grammar's productions. During the process of derivation, there are two kinds of decisions that can be made: | |||
1. Order in which to replace nonterminals in a production, in case the [[#Production_Body|production body]] contains more than one nonterminals. If during this process we constantly pick the leftmost nonterminal for further replacement, the derivation is called the <span id='Leftmost_Derivation'></span>'''leftmost derivation'''. If we constantly pick the rightmost nonterminal, the derivation is called the <span id='Rightmost_Derivation'></span>'''rightmost derivation'''. Rightmost derivations are sometimes called '''canonical derivations'''.<font color=darkgray>The process of building a rightmost derivation tree can be "reversed" by a bottom-up parser.</font>. | |||
2. Which production to pick, in case there are more than one productions associated with a specific nonterminal. | |||
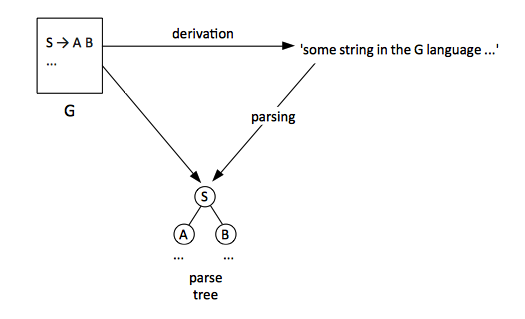
<span id='Parsing'></span>'''Parsing''' is the process of building a [[#Parse_Tree|parse tree]] starting from from a given string of terminals. | |||
:::[[File:DerivationParsing.png]] | |||
<span id='Sentential_Form'></span>If the start symbol S can be derived to an intermediate string containing terminals and nonterminals, in a sequence fo steps, we say that the string obtained as the result of the process is a '''sentential form''' of the grammar. | |||
<span id='Sentence'></span>A '''sentence''' of a grammar G is a [[#Sentential_Form|sentential form]] with no nonterminals. | |||
== | ==Language== | ||
= | <span id='Language'></span>The terminal strings that can be [[#Derivation|derived]] from, or generated by the start symbol of the grammar from the '''language''' defined by the grammar. Conversely, a '''string''' of the language defined by the grammar is any terminal string that can be derived from the start symbol of the grammar. Another definition of a language generated by a grammar is the set of strings that can generated by some [[#Parse_Tree|parse tree]]. | ||
==Parse Tree== | ==Parse Tree== | ||
| Line 47: | Line 78: | ||
A parse tree is a graphical representation of how the [[#Start_Symbol|start symbol]] of a grammar [[#Derivation|derives]] a string in the [[#Language|language]] defined by the grammar. | A parse tree is a graphical representation of how the [[#Start_Symbol|start symbol]] of a grammar [[#Derivation|derives]] a string in the [[#Language|language]] defined by the grammar. | ||
Each interior node of a parse tree represents the application of a [[#Production|production]] and it is labeled with the name of the [[#Nonterminal|nonterminal]] that is the [[#Production_Head|head]] of the production. The children node are labeled, from left to right, by the symbols in the [[#Production_Body|body]] of the production. While is being constructed, the leaves of a parse tree may represent terminals and nonterminals, which at any moment, if they are read from left to right, they constitute the '''yield''' or the '''frontier''' of the tree, and it is also referred to as a '''sentential from''' of the grammar. | The root of the parse tree is labeled by the start symbol. Each interior node of a parse tree represents the application of a [[#Production|production]] and it is labeled with the name of the [[#Nonterminal|nonterminal]] that is the [[#Production_Head|head]] of the production. The children node are labeled, from left to right, by the symbols in the [[#Production_Body|body]] of the production. While is being constructed, the leaves of a parse tree may represent terminals and nonterminals, which at any moment, if they are read from left to right, they constitute the '''yield''' or the '''frontier''' of the tree, and it is also referred to as a '''sentential from''' of the grammar. After a string in the language defined by the grammar is fully parsed, each leaf is labeled by a terminal or by ε. | ||
A parse tree does not contain the information that reflects the order in which productions are applied to replace [[#Nonterminal|nonterminals]]. It is customary to produce parse trees by always producing the [[#Leftmost_Derivation|leftmost]] (or [[#Rightmost_Derivation|rightmost]]) derivation. Each parse tree has associated with it a unique leftmost and an unique rightmost derivation. | A parse tree does not contain the information that reflects the order in which productions are applied to replace [[#Nonterminal|nonterminals]]. It is customary to produce parse trees by always producing the [[#Leftmost_Derivation|leftmost]] (or [[#Rightmost_Derivation|rightmost]]) derivation. Each parse tree has associated with it a unique leftmost and an unique rightmost derivation. | ||
| Line 70: | Line 101: | ||
:[[File:SyntaxTree.png]] | :[[File:SyntaxTree.png]] | ||
<font color=darkgray>TODO: Construction of Syntax Trees, Compilers Book Section 2.8.2.</font> | |||
==<span id='Ambiguity'>Ambiguous Grammars== | |||
A grammar for which more than one [[#Parse_Tree|parse tree]] can be generated from a given string is said to be an '''ambiguous grammar'''. A string with more than more than one parse tree has usually more than one meaning, we need to design unambiguous grammars, or to use additional rules to resolve the ambiguity. | |||
The following grammar is ambiguous because it there are two distinct derivations (parse trees) or the same "NUMBER + NUMBER * NUMBER" string: | |||
''expr'' → ''expr'' + ''expr'' | ''expr'' * ''expr'' | '''NUMBER''' | |||
[[File:AmbigousGrammar.png]] | |||
==<span id='Precedence'></span>Operator Precedence== | ==<span id='Precedence'></span>Operator Precedence== | ||
==Associativity== | Operator precedence refers to the situations when ''different'' operators are applied in the same expression, and parentheses are not involved. | ||
==Operator Associativity== | |||
Operator associativity refers to the situations when the ''same'' operator is applied repeatedly to multiple operands, in the same expression, and parentheses are not involved. | |||
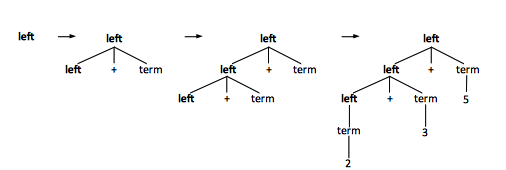
An operator '''associates left''' if an operand with the same operator on both sides belongs to the operator on its left. For example, 2 + '''3''' + 5 is equivalent with (2 + 3) + 5, so 3 belongs to the '+' on its left. An example of grammar for an operator that associates right is: | |||
''left'' → ''left'' '''+''' ''term'' | ''term'' | |||
''term'' → '''NUMBER''' | |||
The parse tree for operators that associate left grows to the left: | |||
[[File:ParseTreeForOperatorThatAssociatesLeft.png]] | |||
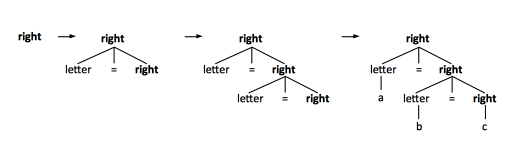
An operator '''associates right''' if an operand with the same operator on both sides belongs to the operator on its right. For example, a = '''b''' = c is equivalent with a = (b = c) so 'b' belongs to the '=' on its right. An example of grammar for an operator that associates right is: | |||
''right'' → ''letter'' '''=''' ''right'' | ''letter'' | |||
''letter'' → [a-z] | |||
The parse tree for operators that associate right grows to the right: | |||
[[File:ParseTreeForOperatorThatAssociatesRight.png]] | |||
==Parser== | ==Parser== | ||
| Line 88: | Line 155: | ||
=Semantic Analysis= | =Semantic Analysis= | ||
Semantic analysis. | |||
Latest revision as of 01:13, 17 September 2021
External
Internal
Overview
Compiler
Interpreter
Programming Language Elements
Variable
Identifier
Statement
Expression
Lexical Analysis
Regular Expressions
Finite Automata
Token
Syntax Analysis (Parsing)
Grammar
A context-free grammar is a formal specification of a language and has four components:
- A set of terminal symbols, or terminals, which are the elementary symbols of the language defined by the grammar and they are sometimes referred to as tokens. Technically, a terminal and the token name are synonymous.
- A set of nonterminals, where each nonterminal represents a set of string of terminals. Nonterminals are sometimes called syntactic variables. Nonterminals impose a hierarchical structure on the language that is key to syntax analysis.
- A set of productions, where each production consists of a nonterminal called production head or left side of the production, an arrow (→ or ::=) and a sequence of terminals and/or nonterminals, called the body or the right side of the production. The components of the body describe one way in which strings of the nonterminal at the head can be constructed. The intuitive intent of a production is to specify one of the written form of a construct - if the head nonterminal represents a construct, then the body represents the written form of the construct. More than one productions may correspond to a specific nonterminal. A production whose right side consists in a single nonterminal is called a single production.
- A start symbol, designated from nonterminals. Conventionally, the production for the start symbol are listed first when the grammar is specified.
One of the possible terminals is ε, which signifies the "empty string".
Left-Recursive Grammar
Relationship to top-down parsers.
Backus-Naur Form (BNF)
Extended Backus-Naur Form (EBNF)
Derivation and Parsing
Derivation is the process of producing a string of terminals using a grammar, beginning with the start symbol and successively replacing nonterminals with their associated productions, until no nonterminals are left. The process can also be thought as building of a parse tree, starting from the grammar rules and advancing towards a tree whose all leafs are terminals, where each internal node of the tree corresponds to a head nonterminal whose production is being processed. A string of the language is generated or derived from the start symbol of the grammar.
The derivation process is recursive, as nonterminals get replaced with other sequences of nonterminals and terminals, as defined by the grammar's productions. During the process of derivation, there are two kinds of decisions that can be made:
1. Order in which to replace nonterminals in a production, in case the production body contains more than one nonterminals. If during this process we constantly pick the leftmost nonterminal for further replacement, the derivation is called the leftmost derivation. If we constantly pick the rightmost nonterminal, the derivation is called the rightmost derivation. Rightmost derivations are sometimes called canonical derivations.The process of building a rightmost derivation tree can be "reversed" by a bottom-up parser..
2. Which production to pick, in case there are more than one productions associated with a specific nonterminal.
Parsing is the process of building a parse tree starting from from a given string of terminals.
If the start symbol S can be derived to an intermediate string containing terminals and nonterminals, in a sequence fo steps, we say that the string obtained as the result of the process is a sentential form of the grammar.
A sentence of a grammar G is a sentential form with no nonterminals.
Language
The terminal strings that can be derived from, or generated by the start symbol of the grammar from the language defined by the grammar. Conversely, a string of the language defined by the grammar is any terminal string that can be derived from the start symbol of the grammar. Another definition of a language generated by a grammar is the set of strings that can generated by some parse tree.
Parse Tree
A parse tree is a graphical representation of how the start symbol of a grammar derives a string in the language defined by the grammar.
The root of the parse tree is labeled by the start symbol. Each interior node of a parse tree represents the application of a production and it is labeled with the name of the nonterminal that is the head of the production. The children node are labeled, from left to right, by the symbols in the body of the production. While is being constructed, the leaves of a parse tree may represent terminals and nonterminals, which at any moment, if they are read from left to right, they constitute the yield or the frontier of the tree, and it is also referred to as a sentential from of the grammar. After a string in the language defined by the grammar is fully parsed, each leaf is labeled by a terminal or by ε.
A parse tree does not contain the information that reflects the order in which productions are applied to replace nonterminals. It is customary to produce parse trees by always producing the leftmost (or rightmost) derivation. Each parse tree has associated with it a unique leftmost and an unique rightmost derivation.
Parse trees are sometimes called concrete syntax trees.
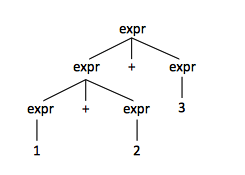
For the following grammar:
expr → expr + expr | NUMBER
and the string "1+2+3", the parse tree is:
(Abstract) Syntax Tree
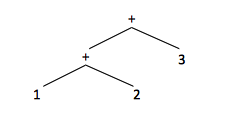
The abstract syntax tree, also referred to as syntax tree, represents the hierarchical syntactic structure of the parsed content, by depicting significant programming constructs. For example, in case of an expression that involves an operator, the fragment of the syntax tree that represents the expression has a node that represents the operator, and its children represent the operands. In general, any programming construct can be handled by marking up an operator for the construct and treating the semantically meaningful components of that construct as operands.
A syntax tree resembles a parse tree to a certain extent. The difference is that for a syntax tree, the internal nodes represent programming constructs, while for parse tree, the internal nodes represent nonterminals. Many nonterminals of a grammar represent programming constructs, but others are intermediate "helpers" of some sort, for example representing terms, factors or other variations of expressions. Examples of productions that are not represented in a syntax tree are expr → term or ε-productions rest → ε. These helpers are dropped into a syntax three. That is why sometimes a parse tree is called a concrete syntax tree.
The corresponding syntax tree of the parse tree represented above is:
TODO: Construction of Syntax Trees, Compilers Book Section 2.8.2.
Ambiguous Grammars
A grammar for which more than one parse tree can be generated from a given string is said to be an ambiguous grammar. A string with more than more than one parse tree has usually more than one meaning, we need to design unambiguous grammars, or to use additional rules to resolve the ambiguity.
The following grammar is ambiguous because it there are two distinct derivations (parse trees) or the same "NUMBER + NUMBER * NUMBER" string:
expr → expr + expr | expr * expr | NUMBER
Operator Precedence
Operator precedence refers to the situations when different operators are applied in the same expression, and parentheses are not involved.
Operator Associativity
Operator associativity refers to the situations when the same operator is applied repeatedly to multiple operands, in the same expression, and parentheses are not involved.
An operator associates left if an operand with the same operator on both sides belongs to the operator on its left. For example, 2 + 3 + 5 is equivalent with (2 + 3) + 5, so 3 belongs to the '+' on its left. An example of grammar for an operator that associates right is:
left → left + term | term term → NUMBER
The parse tree for operators that associate left grows to the left:
An operator associates right if an operand with the same operator on both sides belongs to the operator on its right. For example, a = b = c is equivalent with a = (b = c) so 'b' belongs to the '=' on its right. An example of grammar for an operator that associates right is:
right → letter = right | letter letter → [a-z]
The parse tree for operators that associate right grows to the right:
Parser
Top-Down Parser
A top-down parser is a parser that employs a strategy where it first looks at the highest level of the parse tree and works down the parser tree by using the rewriting rules of the formal grammar. The top-down parser discovers the parse tree starting from the top and incrementally works its way first downwards and then rightwards. Unlike a bottom-up parser, the top-down parser eagerly decides what a construct is much earlier, when it has only scanned the leftmost symbol of that construct and has not yet parsed any of its parts.
If a language grammar has multiple rules that may start with the same leftmost symbols but have different endings, that grammar can be efficiently handled by a deterministic bottom-up parser, but cannot be handled top-down without guesswork and backtracking - so bottom-up parsers handle a somewhat larger range of computer language grammars than top-down parsers.
A recursive descent parsers is a top-down parser build from a set of possibly mutually recursive procedures, where each such procedure usually implements one of the productions of the grammar. In consequence, the structure of the resulting program closely mirrors that of the grammar it recognizes. A predictive recursive descent parser is a recursive descent parser that does not require backtracking, it is called a predictive parser.
Bottom-Up Parser
Semantic Analysis
Semantic analysis.