Stack

Internal

• Data Structures
• Queue
• Deque

Overview

A stack is a dynamic set in which the the DELETE operation, which does not have any argument, removes the most recently inserted element. The stack implements a Last-In-First-Out, or LIFO, policy. The INSERT operation for a stack is called PUSH, and places the element at the top of the stack. The DELETE operation is called POP. If the stack contains no elements it is said to be empty. If POP() operation is invoked on an empty stack, we say that the stack underflows. If PUSH() operation is called on a full stack, we say that the stack overflows.

The stack is an essential component in implementing the iterative Depth-First Search (DFS) algorithm in graphs.

Implementation

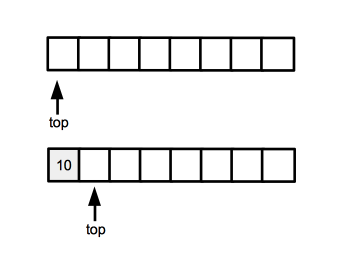
The following code shows how to implement a simple stack of ints, backed by an integer array. The stack capacity is dictated by the length of the array.

/**
 * A stack of ints.
 */
public class Stack {

    private int[] storage;

    //
    // 'top' indicates the first *free* location in storage. 
    // For an empty stack, top is 0 and for a full stack, 
    // top is equal with storage.length
    //
    private int top;

    public Stack(int capacity) {

        this.storage = new int[capacity];
        this.top = 0;
    }

    public void push(int i) throws StackOverflowException {

        if (top == storage.length) {

            throw new StackOverflowException();
        }

        storage[top ++] = i;
    }

    public int pop() throws StackUnderflowException {

        if (top == 0) {

            throw new StackUnderflowException();
        }

        return storage[-- top];
    }

    public boolean isEmpty() {

        return top == 0;
    }

    public boolean isFull() {

        return top == storage.length;
    }
}

Organizatorium

• https://github.com/jwasham/coding-interview-university#stack