Consistent Hashing: Difference between revisions
| (5 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
=Internal= | =Internal= | ||
* [[Data Structures | * [[Data Structures]] | ||
* [[Distributed Hash Table#Consistent_Hashing|Distributed Hash Table]] | |||
* [[Rendezvous Hashing]] | |||
* [[Distributed_Systems#Consistent_Hashing|Distributed Systems]] | |||
=Overview= | =Overview= | ||
The consistent hashing algorithms have been devised specifically to work around the need of moving state in case of of node failure (or node additions) in distributed hash maps. In traditional hashing each key goes into a ''slot'' (or ''bucket'') corresponding to an index calculated applying a hashing function to the key. The index is calculated with the formula <tt>hash(k) % n</tt>, where <tt>k</tt> is the key value and <tt>n</tt> is the number of storage buckets. See [[Hash | The consistent hashing algorithms have been devised specifically to work around the need of moving state in case of of node failure (or node additions) in distributed hash maps. In traditional hashing each key goes into a ''slot'' (or ''bucket'') corresponding to an index calculated applying a hashing function to the key. The index is calculated with the formula <tt>hash(k) % n</tt>, where <tt>k</tt> is the key value and <tt>n</tt> is the number of storage buckets. See [[Hash Table]] for more details. | ||
Applied to caching, each storage bucket corresponds to a physical caching node. This technique allows to distribute load - in this case serving cached content - among multiple physical nodes, hence allowing for horizontal scalability. | Applied to caching, each storage bucket corresponds to a physical caching node. This technique allows to distribute load - in this case serving cached content - among multiple physical nodes, hence allowing for horizontal scalability. | ||
A mod k hash distributes the keys perfectly balanced among a node population but becomes extremely inefficient on node failure or node addition because '''all''' keys have to be rebalanced among nodes (either by direct state transfer among nodes or by flushing the cache and directing the misses to the back end store). Removing a node - as result of a node failure, for example - or adding a node causes the n to change. In consequence, the storage bucket index changes for ''all'' keys, so ''all'' keys must be re-mapped to different storage buckets. When a key is requested after | A mod k hash distributes the keys perfectly balanced among a node population but becomes extremely inefficient on node failure or node addition because '''all''' keys have to be rebalanced among nodes (either by direct state transfer among nodes or by flushing the cache and directing the misses to the back end store). Removing a node - as result of a node failure, for example - or adding a node causes the n to change. In consequence, the storage bucket index changes for ''all'' keys, so ''all'' keys must be re-mapped to different storage buckets. When a key is requested after resizing, the key is initially not found in the new storage bucket, and that leads to a cache miss, and that triggers a request to the origin server. In case of such event, the origin servers (either databases or something else) must serve the entire key population and they are likely to be overloaded. | ||
This issue is solved with ''consistent hashing''. | This issue is solved with ''consistent hashing''. | ||
Latest revision as of 20:19, 5 June 2019
External
- http://en.wikipedia.org/wiki/Consistent_hashing
- http://www.tomkleinpeter.com/2008/03/17/programmers-toolbox-part-3-consistent-hashing/
- http://www.lexemetech.com/2007/11/consistent-hashing.html
- http://www.goworkday.com/2010/03/19/single-word-wangjenkins-hash-concurrenthashmap/
Internal
Overview
The consistent hashing algorithms have been devised specifically to work around the need of moving state in case of of node failure (or node additions) in distributed hash maps. In traditional hashing each key goes into a slot (or bucket) corresponding to an index calculated applying a hashing function to the key. The index is calculated with the formula hash(k) % n, where k is the key value and n is the number of storage buckets. See Hash Table for more details.
Applied to caching, each storage bucket corresponds to a physical caching node. This technique allows to distribute load - in this case serving cached content - among multiple physical nodes, hence allowing for horizontal scalability.
A mod k hash distributes the keys perfectly balanced among a node population but becomes extremely inefficient on node failure or node addition because all keys have to be rebalanced among nodes (either by direct state transfer among nodes or by flushing the cache and directing the misses to the back end store). Removing a node - as result of a node failure, for example - or adding a node causes the n to change. In consequence, the storage bucket index changes for all keys, so all keys must be re-mapped to different storage buckets. When a key is requested after resizing, the key is initially not found in the new storage bucket, and that leads to a cache miss, and that triggers a request to the origin server. In case of such event, the origin servers (either databases or something else) must serve the entire key population and they are likely to be overloaded.
This issue is solved with consistent hashing.
Consistent hashing is a technique where the storage bucket "boundaries" are also calculated by applying a hash function to the storage node identifier or some other attribute of the node - hence each bucket depends on the node itself, and is not a function of all nodes.
The essential difference from traditional hashing is that if one of the storage nodes fails, only the keys stored on that node need to be remapped; the other keys keep living in the remaining valid buckets. The same is true about adding nodes: if a node is added, its storage bucket replaces space allocated previously to other nodes' storage buckets, so some of the keys will be remapped to take advantage of the newly available storage space, but most of the keys will stay in place in their existing storage.
Technique
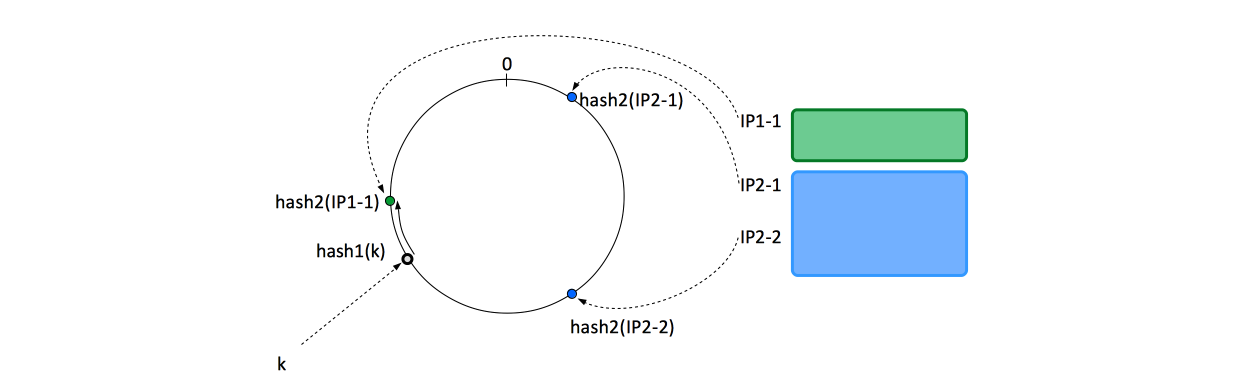
Given a key and a list of storage nodes, this algorithm describes the method of deterministically finding a node to store it onto. It can also be used to find a second (and a third node) for replication. The method is based on mapping each key on the point on the edge of a circle or hash wheel (or equivalently, mapping each key to an angle), by applying a hash function to it. At the same time, each storage bucket (node, physical storage machine, etc.) is allocated a number of formal identifiers. This way, we can model difference in storage capacity among nodes: nodes with more storage available are allocated proportionally more identifiers.
The identifiers are mapped on points on the edge of the same circle, also applying a hash function to it. The hash function applied to keys and storage bucket identifiers do not necessarily have to be the same, only the range of the two functions need to match. When we need to decide what node a specific keys should be stored into, we start from the point on the edge of the circle corresponding to the key in question and we walk clockwise until we find the first node identifier. That will be the storage node used to store the key.
Virtual Nodes
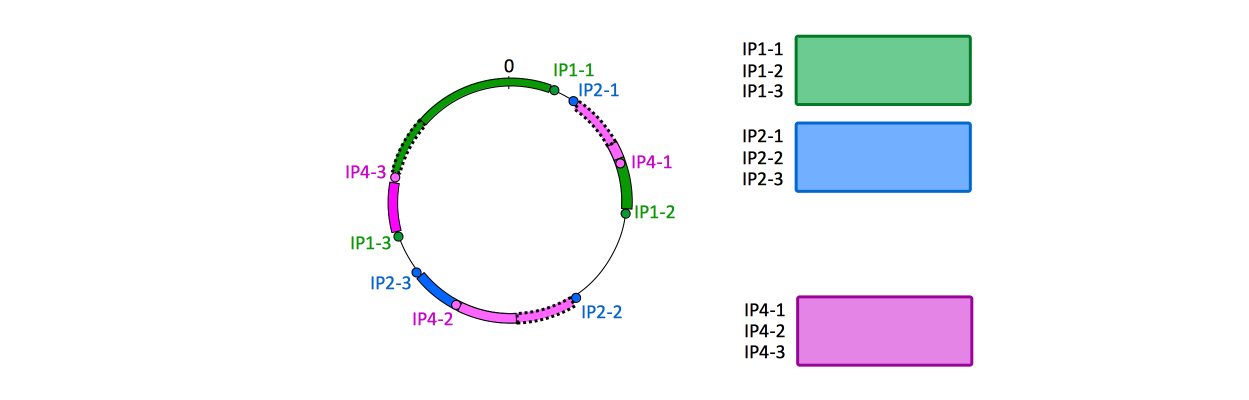
In order to improve the key distribution among nodes, a (usually large) number of distinct virtual nodes are allocated to each physical nodes, so a physical node is virtually spread around the entire hash wheel. In Infinispan, virtual nodes are also referred to as "segments".
What Happens if a Node Disappears
If the primary node for a key fails, the implementation does not need to do anything except update the hash wheel by removing all its virtual node hashes. Upon key retrieval, it simply needs to walk the hash wheel until it encounters the first redundant key, and so on. The process of finding the "secondary physical node", then the "ternary physical node", etc., is deterministic and *does not involve state transfer*, because the keys were already stored upon initial write.
When a physical node fails, all its virtual node projections on the hash wheel disappear as described above, the corresponding keys are lost (the node failed after all), but if "owners" is larger than 1, the keys were previously and redundantly stored on other nodes that are still available. Again, no state transfer required.
What Happens if a new Node is Added
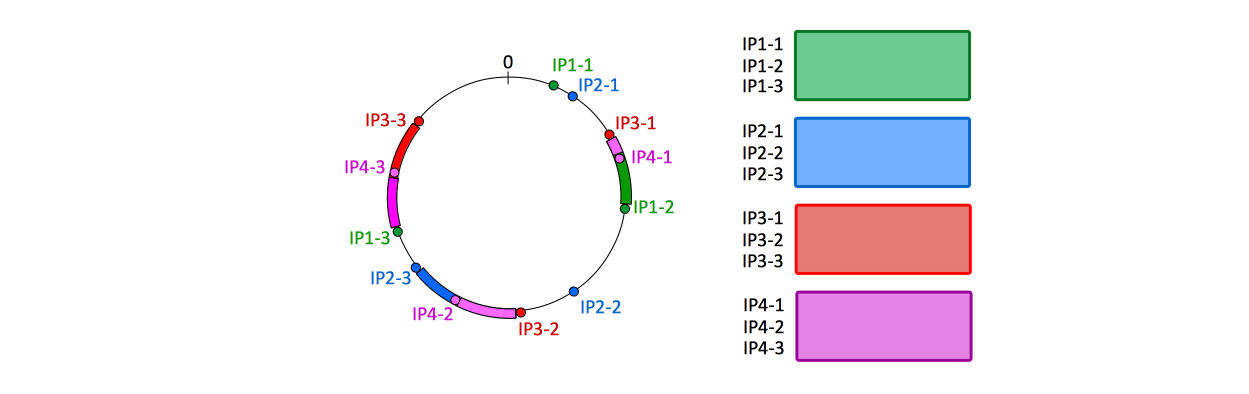
When a new physical node is added, new virtual node hashes are projected on the hash wheel. The storage corresponding to those virtual node is initially empty.
At this point we have a choice:
1) either employ state transfer and re-balancing to preemptively physically move the keys from the section of the hash wheel "eclipsed" by the newly added virtual node to the corresponding physical nodes
or:
2) simply incur the miss for those keys, followed by an update from the backend store.
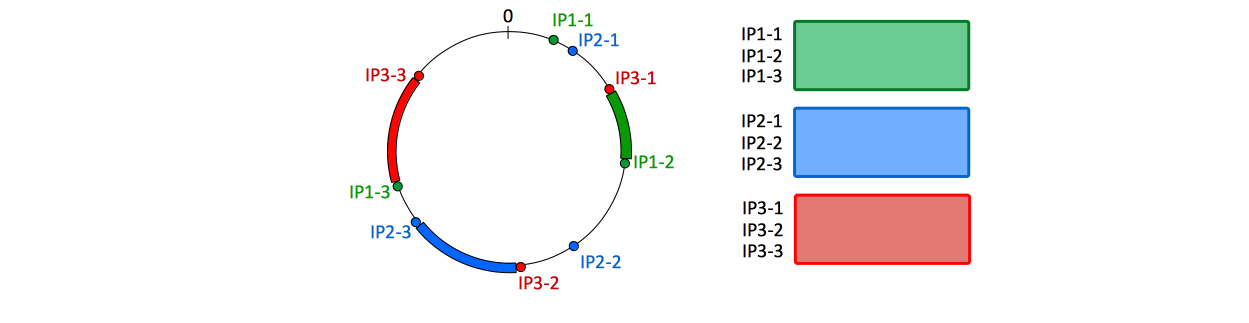
This is how a hash wheel for three nodes (each node having 3 segments) looks like:
This is how the same hash wheel looks like after adding a fourth node (also with 3 segments):
Consistent Hashing and Replication to More than One Node
If we want to replicate a key to more than one node for redundancy (in Infinispan, this is declaring an "owner" value larger than 1), the implementation keeps walking clockwise around the hash wheel until it reaches the next virtual node hash that is does not correspond the physical node the key was stored already. The key is redundantly stored on that physical node too. The process is repeated for each "owner". No specific "replication" (or "state transfer") logic should be required at all to redundantly store keys. The consistent hashing algorithm should just keep walking clockwise around the wheel and replicate the key as many times as instructed.
If the primary node fails, the implementation does not need to do anything except update the hash wheel by removing all its virtual node hashes. Upon retrieval, it simply needs to walk the hash weel until it encounters the first redundant storage, and so on. The process of finding the "secondary physical node", then the "ternary physical node", etc., is deterministic and does not involve state transfer, because the keys were already stored upon initial writing.