Tree Representation in Memory: Difference between revisions
| (20 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
=Overview= | =Overview= | ||
[[Tree_Concepts#Rooted_Tree|Rooted trees]] can be implemented in several ways: | [[Tree_Concepts#Rooted_Tree|Rooted trees]] can be implemented in several ways: | ||
* Use [[#Representing_Rooted_Trees_as_Linked_Data_Structures|linked data structures]] | * Use [[#Representing_Rooted_Trees_as_Linked_Data_Structures|linked data structures]] | ||
* Use | * Use an [[#Representing_Rooted_Trees_in_an_Array|array and a heap structure]] | ||
=Representing Rooted Trees as Linked Data Structures= | =Representing Rooted Trees as Linked Data Structures= | ||
Each tree [[#Node|node]] is represented by an object that has a '''key''' | Each tree [[Tree_Concepts#Node|node]] is represented by an object that has a '''key''' attribute and '''pointers''' to other nodes, which vary depending on the tree type: | ||
== | ==Binary Trees== | ||
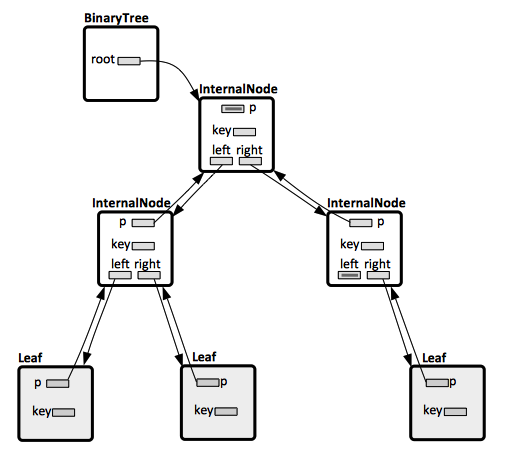
A [[Tree_Concepts#Binary_Tree|binary tree]] node has three pointers: | |||
* | * <code>p</code>, which points to the [[Tree_Concepts#Parent|parent]] node. Only the [[Tree_Concepts#Root|root]] has a NULL parent. | ||
* | * <code>left</code> and <code>right</code>, which point to the left and the right [[Tree_Concepts#Child|child]]. If the node has no left child, <code>left</code> is NULL. If the node has no right child, <code>right</code> is NULL. | ||
:::[[Image:Tree_BinaryTree_Representation.png]] | |||
= | <syntaxhighlight lang='java'> | ||
public class N { | |||
public N p; // parent, may be null for root | |||
public N l; // left child | |||
public N r; // right child | |||
public String k; // key | |||
One option to represent trees whose nodes have an arbitrary number of children is to extend the scheme used for representing binary tree to any class of trees in which the number of children in each node is at most some constant k: we replace the | public N(String k) { | ||
this.k = k; | |||
} | |||
} | |||
</syntaxhighlight> | |||
{{External|https://github.com/ovidiuf/playground/blob/master/algorithms/trees/binary-tree/src/main/java/playground/bt/N.java}} | |||
==Trees whose Nodes have an Arbitrary Number of Children== | |||
One option to represent trees whose nodes have an arbitrary number of children is to extend the scheme used for representing binary tree to any class of trees in which the number of children in each node is at most some constant k: we replace the <code>left</code> and <code>right</code> attributes by <code>child<sub>0</sub></code>, <code>child<sub>1</sub></code>, ... <code>child<sub>k-1</sub></code>. However, this is not ideal: we cannot represent an unbounded number of children, and also when the number of children k is bounded by some large constant, but most nodes have a small number of children, we waste a lot of memory. | |||
Another scheme to represent an arbitrary number of children is '''left-child, right-sibling representation'''. Instead of having a pointer to each of its children, each node has only three pointers: | Another scheme to represent an arbitrary number of children is '''left-child, right-sibling representation'''. Instead of having a pointer to each of its children, each node has only three pointers: | ||
| Line 27: | Line 42: | ||
* right-sibling points to the node's sibling immediately to the right. | * right-sibling points to the node's sibling immediately to the right. | ||
:::[[File:Tree_LeftChild_RightSibling_Represenation.png]] | |||
=Representing Rooted Trees in an Array= | |||
Trees can be represented in memory by using an array where each element of the array contains a pointer to a tree [[Tree_Concepts#Node|node]]. The data structure that represents a tree in an array is called a '''heap'''. | |||
==Binary Heap== | |||
A data structure that represents a [[Tree_Concepts#Binary_Tree|binary tree]] using an array is called a '''binary heap'''. | |||
{{Internal|Heap#Overview|Heaps}} | |||
Latest revision as of 22:46, 10 November 2021
Internal
Overview
Rooted trees can be implemented in several ways:
- Use linked data structures
- Use an array and a heap structure
Representing Rooted Trees as Linked Data Structures
Each tree node is represented by an object that has a key attribute and pointers to other nodes, which vary depending on the tree type:
Binary Trees
A binary tree node has three pointers:
p, which points to the parent node. Only the root has a NULL parent.leftandright, which point to the left and the right child. If the node has no left child,leftis NULL. If the node has no right child,rightis NULL.
public class N {
public N p; // parent, may be null for root
public N l; // left child
public N r; // right child
public String k; // key
public N(String k) {
this.k = k;
}
}
Trees whose Nodes have an Arbitrary Number of Children
One option to represent trees whose nodes have an arbitrary number of children is to extend the scheme used for representing binary tree to any class of trees in which the number of children in each node is at most some constant k: we replace the left and right attributes by child0, child1, ... childk-1. However, this is not ideal: we cannot represent an unbounded number of children, and also when the number of children k is bounded by some large constant, but most nodes have a small number of children, we waste a lot of memory.
Another scheme to represent an arbitrary number of children is left-child, right-sibling representation. Instead of having a pointer to each of its children, each node has only three pointers:
- parent
- left-child points to the leftmost child
- right-sibling points to the node's sibling immediately to the right.
Representing Rooted Trees in an Array
Trees can be represented in memory by using an array where each element of the array contains a pointer to a tree node. The data structure that represents a tree in an array is called a heap.
Binary Heap
A data structure that represents a binary tree using an array is called a binary heap.