Search Tree Rotation: Difference between revisions
| (2 intermediate revisions by the same user not shown) | |||
| Line 11: | Line 11: | ||
=Left Rotation= | =Left Rotation= | ||
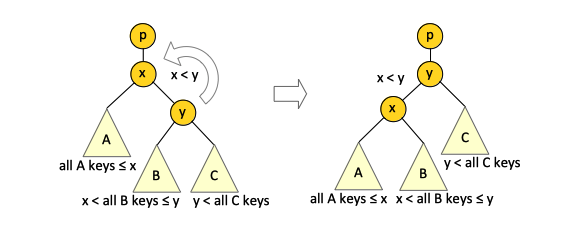
The goal of the left rotation is to invert the relationship between the nodes x and y: y becomes the parent and x the child, while preserving the binary search tree property. | The goal of the left rotation is to invert the relationship between the nodes x and y: y becomes the parent and x the child, while preserving the binary search tree property. | ||
:[[File:Left_Rotation.png]] | :[[File:Left_Rotation.png|581px]] | ||
=Right Rotation= | =Right Rotation= | ||
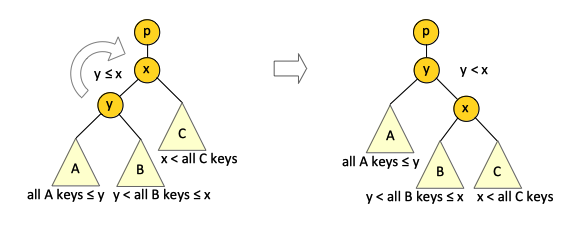
The goal of the right rotation is to invert the relationship between the nodes x and y: y becomes the parent and x the child, while preserving the binary search tree property. | The goal of the right rotation is to invert the relationship between the nodes x and y: y becomes the parent and x the child, while preserving the binary search tree property. | ||
[[File:Right_Rotation.png]] | |||
:[[File:Right_Rotation.png|581px]] | |||
Latest revision as of 19:18, 13 October 2021
External
Internal
Overview
Rotations are a set of primitives common to all binary search tree implementations, which preserve the Binary Search Tree Property while locally rebalancing subtrees at a node in O(1) time. There are left rotations and right rotations. When invoking a rotation, is on a parent-child pair of a search tree. If it is the right child of the parent, use a left rotation. If it is the left child, use a right rotation.
Rotations preserve the Binary Search Tree Property.
Left Rotation
The goal of the left rotation is to invert the relationship between the nodes x and y: y becomes the parent and x the child, while preserving the binary search tree property.
Right Rotation
The goal of the right rotation is to invert the relationship between the nodes x and y: y becomes the parent and x the child, while preserving the binary search tree property.