Hash Table: Difference between revisions
| (16 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
=External= | =External= | ||
* https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/b2Uee/hash-tables-operations-and-applications | * https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/b2Uee/hash-tables-operations-and-applications | ||
* https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/Ob0K7/hash-tables-implementation-details-part-i | * https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/Ob0K7/hash-tables-implementation-details-part-i | ||
| Line 11: | Line 10: | ||
* [[Distributed Hash Table|Distributed Hash Table]] | * [[Distributed Hash Table|Distributed Hash Table]] | ||
* [[Java HashMap]] | * [[Java HashMap]] | ||
* [[Hash Functions]] | |||
=Overview= | =Overview= | ||
Hash tables are one of the most used data structures in programming. They don't have that many operations ([[#INSERT|INSERT()]], [[#DELETE|DELETE()]] and [[#SEARCH|SEARCH()]]), but what they do, they do really well. Conceptually, a hash table is an array that provides immediate random access for [[#Constant_Time|constant time]] insertion, deletion and lookup based on '''an arbitrary key''' and not an integral index, for a dynamic set of keys. The hash map implementations do store data in proper arrays, and the mapping between the arbitrary key and the integral position in the array is provided by a [[#Hash_Functions|hash function]]. Hash maps are some times referred to as [[Data_Structures#Dictionary|dictionaries]], which is fine as long as the dictionary is not assumed to support queries on totally ordered sets: hash maps do not maintain the ordering of the elements that they contain. | Hash tables are one of the most used data structures in programming. They don't have that many operations ([[#INSERT|INSERT()]], [[#DELETE|DELETE()]] and [[#SEARCH|SEARCH()]]), but what they do, they do really well. Conceptually, a hash table is an array that provides immediate random access for [[#Constant_Time|constant time]] insertion, deletion and lookup based on '''an arbitrary key''' and not an integral index, for a dynamic set of keys. The hash map implementations do store data in proper arrays, and the mapping between the arbitrary key and the integral position in the array is provided by a [[#Hash_Functions|hash function]]. Hash maps are some times referred to as [[Data_Structures#Dictionary|dictionaries]], which is fine as long as the dictionary is not assumed to support queries on totally ordered sets: hash maps do not maintain the ordering of the elements that they contain. | ||
A variant of space-inefficient, but extremely time efficient hash table is a [[#Direct-Address_Table|direct-address table]]. | |||
=Canonical Use= | =Canonical Use= | ||
| Line 33: | Line 35: | ||
=Hash Table Implementation Discussion= | =Hash Table Implementation Discussion= | ||
The purpose of a hash table is to maintain a dynamic set of records, each record identified by a unique key, and provide [[#Constant_Time|constant time]] insertion, deletion and search. This is implemented by converting the arbitrary key into a numeric index of a [[#Bucket|bucket]] where the key and the associated value is stored, by applying a hash function to the key. The conversion itself - the hash function running time - should be constant time. | The purpose of a hash table is to maintain a dynamic set of records, each record identified by a unique key, and provide [[#Constant_Time|constant time]] insertion, deletion and search. This is implemented by converting the arbitrary key into a numeric index of a [[#Bucket|bucket]] where the key and the associated value is stored, by applying a [[Hash_Functions#Overview|hash function]] to the key. The conversion itself - the hash function running time - should be constant time. | ||
More formally, we aim to maintain, manage and look up a subset S of a universe of objects U. The cardinality of U is very large, but the cardinality of S is small - thousands, tens of thousand, in general something that fits in the memory of a computer. S is evolving, meaning that we need to add new elements to S and delete existing elements from S. Most importantly, we need to look up elements of S. The idea is that we pick a natural number n, which is close in size to │S│ - the size of S - and we maintain n buckets, where a <span id='Bucket'></span>'''bucket''' is the location in memory where a specific key/value pair is stored. More details on how to choose the number n are available in [[Hash_Functions#Choosing_n|Hash Functions - Choosing n]]. We can use an array A of size n, each element of the array being a bucket. We then choose a hash function: | More formally, we aim to maintain, manage and look up a subset S of a universe of objects U. The cardinality of U is very large, but the cardinality of S is small - thousands, tens of thousand, in general something that fits in the memory of a computer. S is evolving, meaning that we need to add new elements to S and delete existing elements from S. Most importantly, we need to look up elements of S. The idea is that we pick a natural number n, which is close in size to │S│ - the size of S - and we maintain n buckets, where a <span id='Bucket'></span>'''bucket''' is the location in memory where a specific key/value pair is stored. More details on how to choose the number n are available in [[Hash_Functions#Choosing_n|Hash Functions - Choosing n]]. We can use an array A of size n, each element of the array being a bucket. We then choose a hash function: | ||
| Line 49: | Line 51: | ||
===Chaining=== | ===Chaining=== | ||
Each bucket does not merely contain just one element, but contains a linked list of elements that contains the elements that hashed to the same bucket. The list contains in principle an unbounded number of elements. The running time for chaining will be given by the quality of the hash function, a detailed discussion is available in the [[Hash Functions#Overview|Hash Functions]] section. | Each bucket does not merely contain just one element, but contains a linked list of elements that contains the elements that hashed to the same bucket. The list contains in principle an unbounded number of elements. The running time for chaining will be given by the quality of the hash function, a detailed discussion is available in the [[Hash Functions#Overview|Hash Functions]] section. | ||
::[[File:HashTable_Chaining.png|400px]] | |||
===Open Addressing=== | ===Open Addressing=== | ||
Each bucket maintains just one element. In case of a collision, the hash table implementation probes the bucket array for an open position, multiple times if necessary, and keeps trying until it finds an open position. There are multiple strategies to find an open position. One is linear probing: try the next position, and if it is occupied, the next, and so. The second is to use two hashes: the first hash value provides the initial position, and the second hash value provides an offset from the initial position, in case that is occupied. The offset is used repeatedly until an open position is found. The running time for open addressing will be given by the quality of the hash function, a detailed discussion is available in the [[Hash Functions#Overview|Hash Functions]] section. | Each bucket maintains just one element. In case of a collision, the hash table implementation probes the bucket array for an open position, multiple times if necessary, and keeps trying until it finds an open position. There are multiple strategies to find an open position. One is linear probing: try the next position, and if it is occupied, the next, and so. The second is to use two hashes: the first hash value provides the initial position, and the second hash value provides an offset from the initial position, in case that is occupied. The offset is used repeatedly until an open position is found. The running time for open addressing will be given by the quality of the hash function, a detailed discussion is available in the [[Hash Functions#Overview|Hash Functions]] section. | ||
<font color=darkkhaki>[[CLRS]] page 269.</font> | |||
==Load Factor== | ==Load Factor== | ||
There is a very important parameter that plays a big role in the performance of a hash table, and that is the '''load factor''' (or simply, the "load") of a hash table. Is reflects how populated a typical bucket of a hash table is: | There is a very important parameter that plays a big role in the performance of a hash table, and that is the '''load factor''' (or simply, the "load") of a hash table. Is reflects how populated a typical bucket of a hash table is: | ||
| Line 69: | Line 77: | ||
The constant time guarantees applies to properly implemented hash tables. Hash tables are easy to implement badly, on in those case, the constant time guarantee does not hold. | The constant time guarantees applies to properly implemented hash tables. Hash tables are easy to implement badly, on in those case, the constant time guarantee does not hold. | ||
The O(1) running time guarantee is '''on average'''. | The O(1) running time guarantee is '''on average''', assuming [[Hash_Functions#Simple_Uniform_Hashing|simple uniform hashing]]. | ||
The guarantee does not hold for every possible data set. For a specific [[Hash_Functions#Overview|hash function]], there is always a [[Hash_Functions#Pathological_Data_Sets|pathological data set]] for which all elements of the set hash to the same value, and in this case the constant time operations guarantee does not hold. More details about pathological data sets and techniques to work around this issue in [[Hash_Functions#Overview|Hash Functions]] section. | The guarantee does not hold for every possible data set. For a specific [[Hash_Functions#Overview|hash function]], there is always a [[Hash_Functions#Pathological_Data_Sets|pathological data set]] for which all elements of the set hash to the same value, and in this case the constant time operations guarantee does not hold. More details about pathological data sets and techniques to work around this issue in [[Hash_Functions#Overview|Hash Functions]] section. | ||
Another condition for constant running time is that the hash table [[#Load_Factor|load factor]] α must be O(1). If the load factor is a function of n, then intuitively, for a chaining-based implementation, the length of the chaining lists maintained for each bucket will not be constant and will impact the running time. Note that in this case we use a particular notation, n is the number of buckets, '''not the number of elements in the hash table'''. | Another condition for constant running time is that the hash table [[#Load_Factor|load factor]] α must be O(1). If the load factor is a function of n, then intuitively, for a chaining-based implementation, the length of the chaining lists maintained for each bucket will not be constant and will impact the running time. Note that in this case we use a particular notation, n is the number of buckets, '''not the number of elements in the hash table'''. | ||
<font color=darkkhaki>[[CLRS]] Page 258.</font> | |||
=Direct-Address Table= | |||
Direct-address tables make sense when we can afford to allocate an array that has one element for every possible key. This happens when the total number of possible keys is small. To represent a dynamic set, we use an array denoted by T[0 .. m-1], in which each position, or '''slot''', corresponds to a key in the key universe. The array elements store pointers to the object instances corresponding to the keys. If the set contains no element with a key k, then T[k] = NULL. INSERT, DELETE and SEARCH take O(1) time. The disadvantage of using direct-address tables is that if the universe of key is large, allocating an array element for each key is wasteful, and in many cases, impossible, given a computer's memory constraints. | |||
=Distributed Hash Tables= | |||
In case of a distributed hash table, each [[#Bucket|bucket]] may be implemented to reside in a different address space, accessible over the network. This case raises two major problems: a storage node may fail and become unavailable, so a solution for high availability must be implemented, and secondly, hash functions such as [[#Hashing_by_Division|hashing by division]] or [[#Hashing_by_Multiplication|hashing by multiplication]], assume a constant, unchanging number of buckets, and if this number changes, all hash function values become invalid, requiring mass re-distribution, which is an event we must avoid. The problem is addressed by [[Consistent Hashing#Overview|consistent hashing]]. | |||
=Organizatorium= | |||
* https://github.com/jwasham/coding-interview-university#hash-table | |||
Latest revision as of 17:28, 30 June 2022
External
- https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/b2Uee/hash-tables-operations-and-applications
- https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/Ob0K7/hash-tables-implementation-details-part-i
- https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/1Y8t1/hash-tables-implementation-details-part-ii
Internal
Overview
Hash tables are one of the most used data structures in programming. They don't have that many operations (INSERT(), DELETE() and SEARCH()), but what they do, they do really well. Conceptually, a hash table is an array that provides immediate random access for constant time insertion, deletion and lookup based on an arbitrary key and not an integral index, for a dynamic set of keys. The hash map implementations do store data in proper arrays, and the mapping between the arbitrary key and the integral position in the array is provided by a hash function. Hash maps are some times referred to as dictionaries, which is fine as long as the dictionary is not assumed to support queries on totally ordered sets: hash maps do not maintain the ordering of the elements that they contain.
A variant of space-inefficient, but extremely time efficient hash table is a direct-address table.
Canonical Use
Hash tables are used in situations where we need to do repeated fast lookups of arbitrary keys.
- The Deduplication Problem
- The 2-SUM Problem
- Symbol table lookups in compilers
Supported Operations
All operations are O(1) on average. In case the hash table is implemented using chaining, the running time is technically O(list_length). The performance is governed by the length of the chaining lists, and the length of the lists depends on the quality of the hash function.
INSERT(X)
Add a new key/value pair INSERT(X) to the hash map in O(1) running time.
DELETE(K)
Delete a key and the corresponding value DELETE(K) from the hash map in O(1) running time.
SEARCH(K)
Return the value corresponding to the provided key K SEARCH(K), or NULL if the key does not exist, in O(1) running time.
Hash Table Implementation Discussion
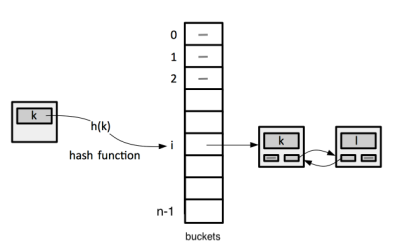
The purpose of a hash table is to maintain a dynamic set of records, each record identified by a unique key, and provide constant time insertion, deletion and search. This is implemented by converting the arbitrary key into a numeric index of a bucket where the key and the associated value is stored, by applying a hash function to the key. The conversion itself - the hash function running time - should be constant time.
More formally, we aim to maintain, manage and look up a subset S of a universe of objects U. The cardinality of U is very large, but the cardinality of S is small - thousands, tens of thousand, in general something that fits in the memory of a computer. S is evolving, meaning that we need to add new elements to S and delete existing elements from S. Most importantly, we need to look up elements of S. The idea is that we pick a natural number n, which is close in size to │S│ - the size of S - and we maintain n buckets, where a bucket is the location in memory where a specific key/value pair is stored. More details on how to choose the number n are available in Hash Functions - Choosing n. We can use an array A of size n, each element of the array being a bucket. We then choose a hash function:
h:U → {0,1,2 ..., n-1}
and we use the hash function result on the object (key) x to select the bucket to store the key and the value in: store x in A[h(x)].
This approach raises the important concept of collision, which is fundamental to hash table implementation: a collision happens when two different keys produce the same hash function result, so they must be stored in the same bucket.
The overall constant time guarantee of the hash table only holds if the hash function is properly implemented, and the data set is non-pathological. What "properly implemented" and "pathological data set" means will be addressed in length in the Hash Functions section. Also see Constant Time Discussion below.
Collisions
A collision happens when applying the hash functions on two different key produces the same result. The consequence of a collision is that we need to sore two different key/value pairs in the same bucket. More formally, a collision is two distinct x, y ∈ U such that h(x) = h(y). There are two techniques to deal with collisions: chaining and open addressing. Some times chaining is going to perform better, some times open addressing is going to perform better. If space is at a premium, open addressing is preferable, because chaining has a space overhead. Deletion is tricker when open addressing is used. Open addressing may perform better in presence of memory hierarchies.
Chaining
Each bucket does not merely contain just one element, but contains a linked list of elements that contains the elements that hashed to the same bucket. The list contains in principle an unbounded number of elements. The running time for chaining will be given by the quality of the hash function, a detailed discussion is available in the Hash Functions section.
Open Addressing
Each bucket maintains just one element. In case of a collision, the hash table implementation probes the bucket array for an open position, multiple times if necessary, and keeps trying until it finds an open position. There are multiple strategies to find an open position. One is linear probing: try the next position, and if it is occupied, the next, and so. The second is to use two hashes: the first hash value provides the initial position, and the second hash value provides an offset from the initial position, in case that is occupied. The offset is used repeatedly until an open position is found. The running time for open addressing will be given by the quality of the hash function, a detailed discussion is available in the Hash Functions section.
CLRS page 269.
Load Factor
There is a very important parameter that plays a big role in the performance of a hash table, and that is the load factor (or simply, the "load") of a hash table. Is reflects how populated a typical bucket of a hash table is:
number of objects in the hash table
α = ──────────────────────────────────────
n
where n is the number of buckets. As more objects are inserted in the hash table, the load grows. Keeping the number of objects in the table fixed as the number of buckets increases has the result of a decrease in load. Hash tables implemented using chaining can have a load factor bigger than 1. Hash tables implemented using open addressing cannot have a load factor bigger than 1, because for open addressing, cannot be more objects than buckets in the hash table. In fact, for open addressing hash tables, the load factor should be maintained to be much less than 1 (α ≪ 1). A discussion on how the load factor influences the running time is available below in the Constant Time Discussion section.
α can be controlled at runtime by increasing (or decreasing) the number of buckets. If the number of buckets is changed, the data must be redistributed.
Hash Functions
Constant Time Discussion
The constant time guarantees applies to properly implemented hash tables. Hash tables are easy to implement badly, on in those case, the constant time guarantee does not hold.
The O(1) running time guarantee is on average, assuming simple uniform hashing.
The guarantee does not hold for every possible data set. For a specific hash function, there is always a pathological data set for which all elements of the set hash to the same value, and in this case the constant time operations guarantee does not hold. More details about pathological data sets and techniques to work around this issue in Hash Functions section.
Another condition for constant running time is that the hash table load factor α must be O(1). If the load factor is a function of n, then intuitively, for a chaining-based implementation, the length of the chaining lists maintained for each bucket will not be constant and will impact the running time. Note that in this case we use a particular notation, n is the number of buckets, not the number of elements in the hash table.
CLRS Page 258.
Direct-Address Table
Direct-address tables make sense when we can afford to allocate an array that has one element for every possible key. This happens when the total number of possible keys is small. To represent a dynamic set, we use an array denoted by T[0 .. m-1], in which each position, or slot, corresponds to a key in the key universe. The array elements store pointers to the object instances corresponding to the keys. If the set contains no element with a key k, then T[k] = NULL. INSERT, DELETE and SEARCH take O(1) time. The disadvantage of using direct-address tables is that if the universe of key is large, allocating an array element for each key is wasteful, and in many cases, impossible, given a computer's memory constraints.
Distributed Hash Tables
In case of a distributed hash table, each bucket may be implemented to reside in a different address space, accessible over the network. This case raises two major problems: a storage node may fail and become unavailable, so a solution for high availability must be implemented, and secondly, hash functions such as hashing by division or hashing by multiplication, assume a constant, unchanging number of buckets, and if this number changes, all hash function values become invalid, requiring mass re-distribution, which is an event we must avoid. The problem is addressed by consistent hashing.