Hash Table

Internal

• Data Structures

Overview

A hash table is a dynamic set that supports INSERT, DELETE and SEARCH - a dictionary.

The simplest, and the most time-efficient implementation of a hash table is a direct address table. However, this implementation is in most cases inefficient from the point of view of allocated space. A much more practical implementation uses an array whose length is proportional with the number of keys actually stored.

Direct-Address Table

Direct-address tables make sense when we can afford to allocate an array that has one element for every possible key. This happens when the total number of possible keys is small. To represent a dynamic set, we use an array denoted by T[0 .. m-1], in which each position, or slot, corresponds to a key in the key universe. The array elements store pointers to the object instances corresponding to the keys. If the set contains no element with a key k, then T[k] = NULL. INSERT, DELETE and SEARCH take O(1) time. The disadvantage of using direct-address tables is that if the universe of key is large, allocating an array element for each key is wasteful, and in many cases, impossible, given a computer's memory constraints.

Hash Table

When the number of keys actually stored is small relative to the total number of possible keys, a hash table is much more effective alternative to a direct-address table. A hash table uses an array whose length is proportional to the number of keys actually stored.

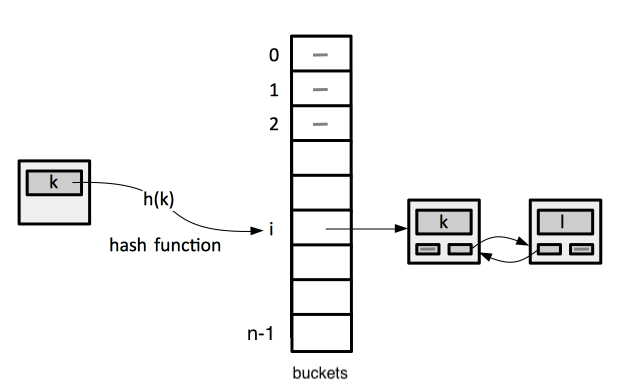
The index of the array element used to store a key, or a pointer to the object containing the key and other data, is computed from the key using a hash function h(k). The array element used to store a key is called slot, or bucket. We say that an element with key k hashes to slot h(k). We also say that h(k) is the hash value of key k.

Collisions are possible. A collision is the situation in which more than one key maps on the same slot. There are different techniques to handle those. Chaining is the most common. Open addressing is another way.

Hash Functions

The hash function h() maps the universe U of keys to the slots of the hash table T[0 ... m-1], where the size m of the hash table is typically much smaller than the size of U:

h : U → {0, 1, ..., m-1}

A hash functions must be deterministic, in that a given input k must always produce the same output h(k). A well designed hash function must also minimize the number of collisions. This can be achieved if each key is equally likely to hash to any of the m slots, independently of where any other key has hashed to. This behavior is called simple uniform hashing. Typically we have no way to check this condition, as we rarely know the probability distribution from which the keys are drawn. Moreover, the key might not be drawn independently. A good approach derives the hash value in a way that we expect to be independent of any patterns that might exist in the data.

Keys as Natural Numbers. All hash functions described below (hashing by division, hashing by multiplication, etc.), assume that the keys are mapped to natural numbers, by some method. When the keys are natural numbers themselves, there is nothing more to be done. However, when the keys are strings, for example, they can be mapped to natural numbers by interpreting them as an integer expressed in a suitable radix notation: each character is expressed as its corresponding 0-127 ASCII code and the position of the character in the string dictates the power 128 is raised to. The result is a natural number, which can grow quite large for long strings. In the context of an application, we can usually devise some method of translating a key into a natural number. The Java Object's hashCode() is aimed to provide this functionality - mapping an object key to an integer numbers.

Hashing by Division

The division method computes the hash value as the remainder when the key value is divided by a specified prime number. This gives good results if we choose a prime number that is unrelated to any patterns in the distribution of keys. We assume that a non-natural key has been mapped to an natural number using the approach described in the Keys as Natural Numbers section.

Collision Handling Techniques

Chaining

Chaining is implemented by placing all elements that hash to the same slot in a linked list, usually at the head. The slot contains a pointer to the head of the list, or NULL.

The implementation of INSERT, DELETE and SEARCH operations is similar to:

TODO - implement.

Note that for INSERT and SEARCH we need to scan the linked list. In case of INSERT, we want to know if the element with the given key isn't already in the list. For DELETE, if the list is doubly-linked, the operation is O(1) - note that the operation takes as input the element and not its key.

Time and Space Complexity for Hash Table with Chaining

In the worst case, searching an element in a hash table can take as long as the search in a linked list Θ(n). However, on average SEARCH, INSERT and DELETE operations take O(1). The space requirements is Θ(|K|), where K is the set of keys actually stored.

TODO

Open Addressing

Open addressing is a technique employed when we need to deal with collisions in a hash table.

Perfect Hashing

Perfect hashing can support searches in O(1) worst-case time, when the set of keys being stored is static - the set of keys never changes once it is stored.

TODO

TODO Hash Map