Tree Representation in Memory: Difference between revisions
| Line 8: | Line 8: | ||
=Representing Rooted Trees as Linked Data Structures= | =Representing Rooted Trees as Linked Data Structures= | ||
Each tree [[Tree_Concepts#Node|node]] is represented by an object that has a '''key''' attribute and '''pointers''' to other nodes, which vary depending on the tree type | Each tree [[Tree_Concepts#Node|node]] is represented by an object that has a '''key''' attribute and '''pointers''' to other nodes, which vary depending on the tree type: | ||
== | ==Binary Trees== | ||
There are three pointers: | There are three pointers: | ||
| Line 18: | Line 18: | ||
<center>[[Image:Tree_BinaryTree_Representation.png]]</center> | <center>[[Image:Tree_BinaryTree_Representation.png]]</center> | ||
== | ==Trees whose Nodes have an Arbitrary Number of Children== | ||
One option to represent trees whose nodes have an arbitrary number of children is to extend the scheme used for representing binary tree to any class of trees in which the number of children in each node is at most some constant k: we replace the ''left'' and ''right'' attributes by ''child<sub>0</sub>'', ''child<sub>1</sub>'', ... ''child<sub>k-1</sub>''. However, this is not ideal: we cannot represent an unbounded number of children, and also when the number of children k is bounded by some large constant, but most nodes have a small number of children, we waste a lot of memory. | One option to represent trees whose nodes have an arbitrary number of children is to extend the scheme used for representing binary tree to any class of trees in which the number of children in each node is at most some constant k: we replace the ''left'' and ''right'' attributes by ''child<sub>0</sub>'', ''child<sub>1</sub>'', ... ''child<sub>k-1</sub>''. However, this is not ideal: we cannot represent an unbounded number of children, and also when the number of children k is bounded by some large constant, but most nodes have a small number of children, we waste a lot of memory. | ||
Revision as of 21:28, 9 October 2021
Internal
Overview
Rooted trees can be implemented in several ways:
- Use linked data structures
- Use a heap structure in an array
Representing Rooted Trees as Linked Data Structures
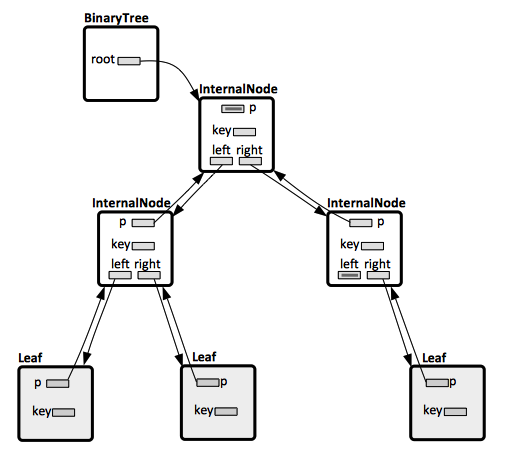
Each tree node is represented by an object that has a key attribute and pointers to other nodes, which vary depending on the tree type:
Binary Trees
There are three pointers:
- p, which points to the parent node. Only the tree's root has a null parent.
- left and right, which point to the left and the right child. If the node has no left child, left is NULL. If the node has no right child, right is NULL.
Trees whose Nodes have an Arbitrary Number of Children
One option to represent trees whose nodes have an arbitrary number of children is to extend the scheme used for representing binary tree to any class of trees in which the number of children in each node is at most some constant k: we replace the left and right attributes by child0, child1, ... childk-1. However, this is not ideal: we cannot represent an unbounded number of children, and also when the number of children k is bounded by some large constant, but most nodes have a small number of children, we waste a lot of memory.
Another scheme to represent an arbitrary number of children is left-child, right-sibling representation. Instead of having a pointer to each of its children, each node has only three pointers:
- parent
- left-child points to the leftmost child
- right-sibling points to the node's sibling immediately to the right.
