Heap

External

• https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/iIzo8/heaps-operations-and-applications
• https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/KKqlm/heaps-implementation-details-advanced-optional

Internal

• Data Structures
• Tree Concepts
• Tree Representation in Memory
• Heap Sort

Overview

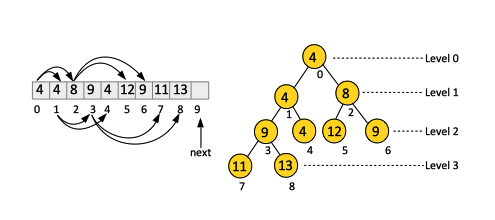
This article is about binary heaps. Heaps are also known as priority queues.A binary heap data structure is an array where data is placed to form a binary tree as complete as possible, plus the index of the last node in the heap. Each element of the array contains a pointer to the actual tree nodes. Each node contains at least a key. The heap works by comparing key and placing the pointer of the associated nodes in the right position in the array. Duplicate key values are supported. For more details on representation in memory, see the Representation in Memory section below.

The heap data structure maintains an invariant, which is called the heap property.

More details CLRS page 151, page 1177.

The Min Heap Property

For every node x, key[x] ≤ all keys of its children.

In case of a max heap, the invariant inequality is reversed.

Note that the Heap Property is different from the Binary Search Tree Property. Heaps are designed to find the minimum (or maximum) easily, unlike the search tree that are designed so we can search easily through them.

Canonical Uses of a Heap

The primary reason to use a heap is if you notice that your program does repeated minimum (maximum) computations, usually via exhaustive search. The heap naturally maintains the minimum (maximum) in reach of an O(1) lookup, while insertions and deletions are O(log n).

Maintaining the minimum (maximum) efficiently is useful in:

• Heap Sort
• The Median Maintenance Problem
• Speed up Dijkstra's Algorithm

Supported Operations

INSERT

Insert a node in the tree. The running time is O(log n) where n is the number of nodes. For implementation, see INSERT Implementation below.

Also see:

Data Structures | INSERT

INSERT Implementation

When a new key is presented, place it on the first available position at the end of the array. We need to do this to maintain the tree as balanced as possible.

If the new key is larger or equal to its parent, no more operations are necessary.

If the new key is smaller than its parent, leaving it on the current position would violate the heap property, so we need to work to restore the invariant. We do this by bubbling it up through the array: repeatedly comparing the key with its parent, and swapping their positions, until we find a parent that is smaller than the key. It the worst case, we need to advance all the way to the root of the tree and swap that. Since the tree is balanced, in the worst case we need to perform log n steps.

REMOVE-MIN

Remove the node from the heap with minimum key value. This operation is available only on a min heap. The running time is O(log n) where n is the number of nodes. For implementation see REMOVE-MIN Implementation below.

Also see:

Data Structures | DELETE

Min Heap and Max Heap

A heap is constructed in such a way that it maintains a minimum value or a maximum value, but not both. A heap that maintains the minimum value is called a min heap and supports the REMOVE-MIN operation. A heap that maintains the maximum value is called a max heap and supports the REMOVE-MAX operation. If both extracting minimum and maximum are required, use a binary search tree instead.

Note that if we know all numbers to be inserted in a heap are positive, a max heap can be implemented using a min heap and storing the negative values.

REMOVE-MIN Implementation

Remove the root and return it, but not before fixing the tree, as follows.

Take the last node added as leaf and promoted it to root.

This may break the heap property - if the new key is larger than any of its children.

If the heap property is broken, swap the key with the smallest child and repeat the procedure by bubbling the key down through the tree until there is no more heap property violation.

HEAPIFY

Initialize the heap in linear time O(n). Using INSERT would take O(n log n), but HEAPIFY does it in O(n) when invoked on a batch of n elements.

TODO

DELETE

Delete an arbitrary node in the middle of the heap in O(log n) time. This is useful when implementing Dijkstra's Algorithm

Also see:

Data Structures | DELETE

TODO

Representation in Memory

A heap has two representations: the physical representation is an array; the conceptual representation is a rooted binary tree, as complete as possible.

For each node i, the left children is stored in the 2i+1 element of the array, and the right children is stored in the 2i + 2 element of the array.

Conversely, for a node i, the parent is stored at ⌊(i - 1)/2⌋.

The advantage of the heap array representation is that rather than traversing pointers, it is very fast to just go from a node to its parent or to either one of its children by doing index arithmetic with bit shifting. Also, we don't need the overhead of storing references.

The fact that the binary tree is as complete as possible (the nodes are added layer by layer, and left to right) is essential for the heap array representation.

Comparison between a Balanced Binary Search Tree and a Heap

Comparison between a Balanced Binary Search Tree and a Heap

Playground Implementation

https://github.com/ovidiuf/playground/blob/master/learning/stanford-algorithms-specialization/06-median-maintenance/src/main/java/playground/stanford/mm/MinHeap.java