Queue

Internal

• Data Structures
• Stack

Overview

A queue is a dynamic set in which the the DELETE operation, which does not have any argument, removes the oldest element in the queue. The queue implements the first-in-first-out, or FIFO, policy. The queue has a head and a tail. The INSERT operation for a queue is called ENQUEUE and places the new element at the tail. The DELETE operation is called DEQUEUE, and has no argument. It simply returns the element at the head of the queue, if any. If we attempt to dequeue an element from an empty queue, it is said that the queue underflows. If we attempt to enqueue an element on a full queue, it is said that the queue overflows.

Implementation

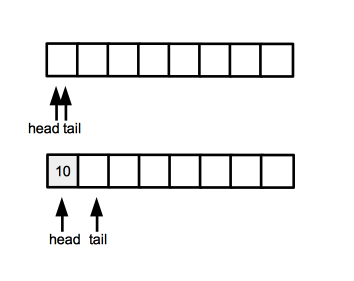
The following implementation uses an array, which dictates the queue length. The queue grows circularly and wraps around the edge of the array as the data is enqueued and dequeued. We use to pointers, "head" and "tail", containing the indexes of the corresponding head and tail elements. The "head" pointer indicates the head element - the one that will be dequeued next, while "tail" points to the position where the next enqueued element will be placed.

An empty queue is indicated by the fact that the "head" and the "tail" pointers have the same value.

We have two choices when it comes to model a full queue. If we want to use all the n elements in the array for queue element storage, then we model the "full" position with an external boolean, because otherwise there would be no way to distinguish the "empty queue" head and tail overlap and "full queue" head and tail overlap. Another possibility is to use only n - 1 elements of the array for queue element storage, and use one array element as a "marker" that always separates the head from the tail. This way, the "head" and "tail" pointers never overlap for a full queue, just for an empty queue.

The equivalent implementations are presented below:

n element Queue

We model "full" and "empty" by allowing the "head" and "tail" markers to overlap, and we maintain an extra bit of data that tells those states apart. This way we can use all n array elements for queue element storage.

/**
 * A queue of ints that uses all n storage elements for queue element storage.
 * It needs an additional boolean variable to maintain whether the queue is 
 * full or not.
 */
public class Queue {

    private int[] storage;

    // this is the index of the queue head element
    private int head;

    // this is the index of the element where the tail *would* go
    private int tail;

    private boolean full;

    public Queue(int capacity) {

        this.storage = new int[capacity];
        this.head = 0;
        this.tail = 0;
        this.full = false;
    }

    public void enqueue(int i) throws QueueOverflowException {

        //
        // check if the queue is full
        //

        if (full) {

            throw new QueueOverflowException();
        }

        storage[tail] = i;

        tail = (tail + 1) % storage.length;

        //
        // this is the only time we can determine the queue is full
        //

        if (head == tail) {

            this.full = true;
        }
    }

    public int dequeue() throws QueueUnderflowException {

        if (head == tail && !full) {

            throw new QueueUnderflowException();
        }

        int result = storage[head];

        head = (head + 1) % storage.length;

        full = false;

        return result;
    }

    public boolean isEmpty() {

        return head == tail;
    }

    public boolean isFull() {

        return full;
    }
}

n-1 element Queue

We model by allowing the "head" and "tail" markers to overlap, and the full queue will always have a gap between head and tail. This way we can use only n-1 array elements for queue element storage.

/**
 * A queue of ints that uses just n-1 storage elements for queue element storage, and
 * it can tell when it is full without maintaining an additional boolean variable.
 */
public class Queue {

    private int[] storage;

    // this is the index of the queue head element
    private int head;

    // this is the index of the element where the tail *would* go
    private int tail;

    public Queue(int capacity) {

        this.storage = new int[capacity];
        this.head = 0;
        this.tail = 0;
    }

    public void enqueue(int i) throws QueueOverflowException {

        //
        // verify whether by enqueueing this element the tail will overlap with the head
        // if they do, it means the queue is full
        //

        if ((tail + 1) % storage.length == head) {

            throw new QueueOverflowException();
        }

        storage[tail] = i;

        tail = (tail + 1) % storage.length;
    }

    public int dequeue() throws QueueUnderflowException {

        if (head == tail) {

            throw new QueueUnderflowException();
        }

        int result = storage[head];

        head = (head + 1) % storage.length;

        return result;
    }

    public boolean isEmpty() {

        return head == tail;
    }

    public boolean isFull() {

        return (tail + 1) % storage.length == head;
    }
}