The Partition Subroutine: Difference between revisions
| Line 11: | Line 11: | ||
We do not insist that we get the relative order correct amongst those elements less than the pivot or amongst those elements that are bigger than the pivot. We do just a partial sorting. Partitioning is a more modest goal than sorting but it makes progress towards sorting - we end up with the pivot in its right position. | We do not insist that we get the relative order correct amongst those elements less than the pivot or amongst those elements that are bigger than the pivot. We do just a partial sorting. Partitioning is a more modest goal than sorting but it makes progress towards sorting - we end up with the pivot in its right position. | ||
The partition subroutine is an essential part of the [[Quicksort#Algorithm|Quicksort]] algorithm. | The partition subroutine is an essential part of the [[Quicksort#Algorithm|Quicksort]] algorithm and also of the [[Selection_Problem#Randomized_Selection|randomized selection problem]]. | ||
=Implementation= | =Implementation= | ||
Latest revision as of 23:30, 27 September 2021
Internal
Problem Statement
Given an array and an element of it - the pivot element - rearrange the array so it has the following property: any element that is at the left of the pivot should be smaller or equal with the pivot, and any element that is at the right of the pivot should be grater that the pivot.
Discussion
After partitioning, the pivot element ends up in its rightful position in the (eventually, but not by this subroutine) sorted array. The implementation is quick (linear time) and in-place.
We do not insist that we get the relative order correct amongst those elements less than the pivot or amongst those elements that are bigger than the pivot. We do just a partial sorting. Partitioning is a more modest goal than sorting but it makes progress towards sorting - we end up with the pivot in its right position.
The partition subroutine is an essential part of the Quicksort algorithm and also of the randomized selection problem.
Implementation
This implementation assumes the pivot is the first element in the array. This choice does not come with loss of generality because if we want a different pivot, we can just simply swap the chosen pivot element with the first element, and the implementation presented below can be applied unchanged.
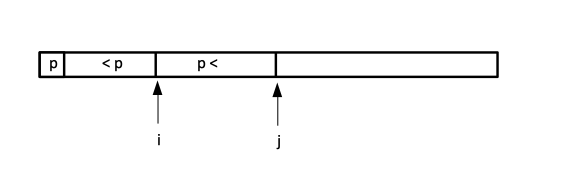
We do a single linear scan and when we maintain two indices: i is the partition boundary- the split between smaller or equal than pivot and larger than pivot - in the section of the array containing the element we've seen so far, and j points to the section of the array we have not seen so far.
We maintain the following invariant: everything we looked at so far is already partitioned.
public static void partition(int[] a, int first, int last) {
// fix the pivot
int pivot = a[first];
int i = first + 1;
// linear scan over the rest of the array
for(int j = first + 1; j <= last; j ++) {
if (a[j] <= pivot) {
// swap
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
i ++;
}
}
// place the pivot in the final position
a[first] = a[i - 1];
a[i - 1] = pivot;
}