Recursion Trees: Difference between revisions
| Line 11: | Line 11: | ||
::[[File:Recursion_Tree.png|1024px]] | ::[[File:Recursion_Tree.png|1024px]] | ||
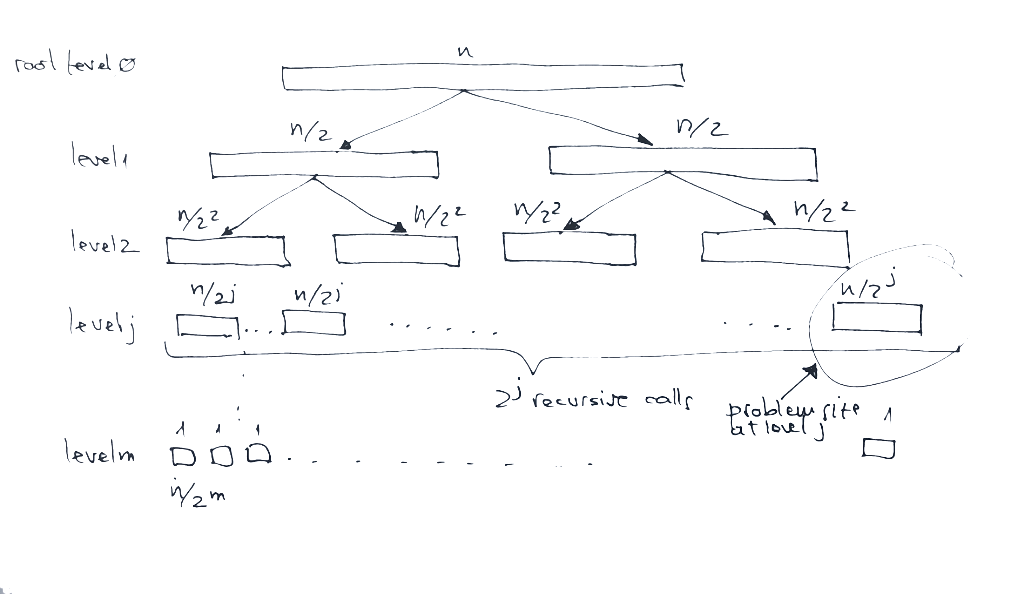
The tree has 1 + log<sub>2</sub>n levels: the bottom-most level m is equals to log<sub>2</sub>n because the problem size | The tree has 1 + log<sub>2</sub>n levels: the bottom-most level m is equals to log<sub>2</sub>n because the problem size decreases by a factor of 2 at each level of recursion, and the bottom-most level problem size is 1, so: | ||
<font size=-1> | <font size=-1> | ||
1 = n/2<sup>m</sup> → n = 2<sup>m</sup> → m = log<sub>2</sub>n | 1 = n/2<sup>m</sup> → n = 2<sup>m</sup> → m = log<sub>2</sub>n | ||
Latest revision as of 18:43, 29 September 2021
Internal
Overview
The idea behind the recursion tree method is to write out the work done by the recursive algorithm in a tree structure, where the children of a given node represent the recursive calls made by that node. The tree will facilitate counting the overall work done by the algorithm and facilitate the analysis. Each node can be annotated with costs incurred at various level of the recursion. After we lay out the tree, we sum the costs within each level of the tree to obtain a set of per-level costs, then we sum all the per-level costs to determine the total cost of the recursion. The bound such guessed can be proven with the substitution method.
Recursion Tree Example for Merge Sort
For merge sort, at each level we sub-divide the problem in 2, we sort recursively, and then we merge the results of the recursive calls with a Θ(n) procedure. If we represent each recursive call as a level in a tree, where the nodes represent the size of the subproblems, we get something similar to:
The tree has 1 + log2n levels: the bottom-most level m is equals to log2n because the problem size decreases by a factor of 2 at each level of recursion, and the bottom-most level problem size is 1, so:
1 = n/2m → n = 2m → m = log2n
The analysis reveals that at the level j of the recursion there are 2j subproblems and each subproblem has a size of n/2j.
The total amount of work done by the algorithm at level j is proportional with the numbers of subproblems and the amount of work per subproblem:
n
2j c ──── = c n = Θ(n)
2j
The total amount of work is:
(1 + log2n)⋅c⋅n = Θ(n log2n)