Tree Concepts: Difference between revisions
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
=Overview= | =Overview= | ||
A tree is a particular case of a [[Graph_Concepts#Graph_Definition|graph]]. | A tree is a particular case of a [[Graph_Concepts#Graph_Definition|graph]]. | ||
=Free Tree= | |||
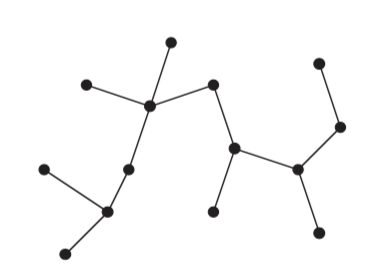
A '''free tree''' is a [[Graph_Concepts#Free_Tree|connected, acyclic, undirected graph]]. | |||
:::[[Image:Graph_FreeTree.png]] | |||
For an undirected graph G = (V, E), the following statements are equivalent: | |||
# G is a free tree. | |||
# Any two vertices in G are connected by a unique [[Graph_Concepts#Simple_Path|simple path]]. | |||
# G is [[Graph_Concepts#Connectivity_and_Graph_Components|connected]], but if any edge is removed from E, the resulting graph is disconnected. | |||
# G is connected and |E| = |V| - 1. | |||
# G is acyclic and |E| = |V| - 1. | |||
# G is acyclic, but if any edge is added to E, the resulting graph contains a cycle. | |||
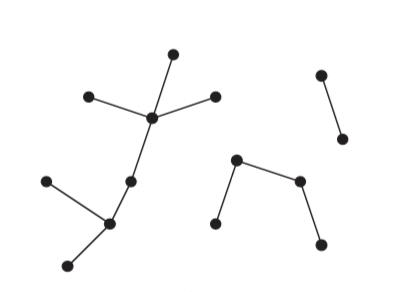
If the undirected graph is acyclic, but [[Graph_Concepts#Connectivity_and_Graph_Components|disconnected]], it is a [[Graph_Concepts#Forest|forest]]. | |||
:::[[Image:Graph_Forest.png]] | |||
=Search Tree= | =Search Tree= | ||
Revision as of 20:35, 9 October 2021
Internal
Overview
A tree is a particular case of a graph.
Free Tree
A free tree is a connected, acyclic, undirected graph.
For an undirected graph G = (V, E), the following statements are equivalent:
- G is a free tree.
- Any two vertices in G are connected by a unique simple path.
- G is connected, but if any edge is removed from E, the resulting graph is disconnected.
- G is connected and |E| = |V| - 1.
- G is acyclic and |E| = |V| - 1.
- G is acyclic, but if any edge is added to E, the resulting graph contains a cycle.
If the undirected graph is acyclic, but disconnected, it is a forest.