Binary Search Trees: Difference between revisions
| Line 24: | Line 24: | ||
<font color=darkkhaki>TODO [[CLRS]] Page 286.</font> | <font color=darkkhaki>TODO [[CLRS]] Page 286.</font> | ||
=Supported Operations= | |||
{| class="wikitable" style="text-align: left;" | |||
! Operation | |||
! Running Time | |||
! Notes | |||
|- | |||
| <span id='INSERT'></span>[[Data_Structures#INSERT.28X.29|INSERT(X)]] || O(log n) || [[#INSERT_Implementation|INSERT Implementation]] | |||
|- | |||
| <span id='DELETE'></span>[[Data_Structures#DELETE.28X.29|DELETE(X)]] || O(log n) || [[#DELETE_Implementation|DELETE Implementation]] | |||
|- | |||
| <span id='SEARCH'></span>[[Data_Structures#SEARCH.28K.29|SEARCH(K)]] || O(log n) || [[#SEARCH_Implementation|SEARCH Implementation]] | |||
|- | |||
| <span id='SELECT'></span>[[Data_Structures#SELECT|SELECT(i<sup>th</sup> order statistics)]] || O(log n) || [[#SELECT_Implementation|SELECT Implementation]] | |||
|- | |||
| [[Data_Structures#MINIMUM.28.29|MINIMUM()]] || O(log n) || [[#MINIMUM_Implementation|MINIMUM Implementation]] | |||
|- | |||
| [[Data_Structures#MAXIMUM.28.29|MAXIMUM()]] || O(log n) || [[#MAXIMUM_Implementation|MAXIMUM Implementation]] | |||
|- | |||
| <span id='PREDECESSOR'></span>[[Data_Structures#PREDECESSOR.28X.29|PREDECESSOR(X)]] || O(log n) || [[#PREDECESSOR_Implementation|PREDECESSOR Implementation]] | |||
|- | |||
| [[Data_Structures#SUCCESSOR.28X.29|SUCCESSOR(X)]] || O(log n) || [[#SUCCESSOR_Implementation|SUCCESSOR Implementation]] | |||
|- | |||
| <span id='RANK'></span>[[Data_Structures#RANK|RANK(X)]] || O(log n) || [[#RANK_Implementation|RANK Implementation]] | |||
|- | |||
|} | |||
==<tt>SEARCH</tt> Implementation== | |||
<font size=-1> | |||
SEARCH(root, X) | |||
</font> | |||
<font size=-1> | |||
SEARCH(n, X) | |||
if X == value(n) return n | |||
if X < value(n) | |||
if there is no left child return NULL | |||
else SEARCH(left_child(n), X) | |||
if X > value(n) | |||
if there is no right child return NULL | |||
else SEARCH(right_child(n), X) | |||
</font> | |||
The running time is Θ(tree_height). | |||
==<tt>INSERT</tt> Implementation== | |||
One implementation, that does not care about keeping the tree balanced, uses the [[#SEARCH_Implementation|recursive search procedure]] described above to keep searching for the key to be inserted until a NULL child pointer is encountered. At that point, the procedure wires a new tree node in that position: | |||
<font size=-1> | |||
INSERT(root, X) | |||
</font> | |||
<font size=-1> | |||
INSERT(n, X) | |||
if X <= value(n) | |||
if there is no left child wire X as left child | |||
else INSERT(left_child(n), X) | |||
if X > value(n) | |||
if there is no right child wire X as right child | |||
else INSERT(right_child(n), X) | |||
</font> | |||
The running time is Θ(tree_height). | |||
==<tt>DELETE</tt> Implementation== | |||
The <code>[[#DELETE|DELETE(X)]]</code> function gets as argument the node to delete. The <code>DELETE(K)</code> function gets as argument the key to delete and in this case we need to locate the node X corresponding to the given key K with <code>[[#SEARCH|SEARCH(K)]]</code>. If no such node exists, nothing is deleted. | |||
To continue, we assume the node X exists. | |||
There are three distinct cases that need to be handled: | |||
1. X has no children. This is the easiest case, the node is just simply deleted from the three. | |||
2. X has just one child - a left child or a right child. In this case, splice out the node to delete, which creates a hole in the tree, and then rewire its child into its parent. The unique child assumes the position of the deleted node. | |||
3. X has both the left and right child. Find the predecessor of the node to be deleted using the <code>[[#PREDECESSOR|PREDECESSOR()]]</code> function. Since X has both left and right subtrees, the predecessor will be the rightmost leaf of its left subtree, as explained in [[#PREDECESSOR_Implementation|PREDECESSOR Implementation]]. Then splice out the node to be deleted and wire the predecessor such found in its place. If the predecessor node has a left child, you may need to wire it into its parent. | |||
==<tt>MINIMUM</tt> Implementation== | |||
Search for -∞: Start with the root and follow the left child until the leftmost leaf. The running time is Θ(tree_height). | |||
==<tt>MAXIMUM</tt> Implementation== | |||
Search for +∞: Start with the root and follow the right child until the rightmost leaf. The running time is Θ(tree_height). | |||
==<tt>PREDECESSOR</tt> Implementation== | |||
Computing the predecessor of a node X in a binary search tree involves finding the node whose key is the next smaller element relative to the X's key. | |||
If the argument to the <code>PREDECESSOR()</code> function is the key itself, the implementation first must search the tree and find the corresponding node. If no node is found, the problem has no solution. | |||
To continue, we assume that the node corresponding to the given key K is found in the tree, and it is X. Computing the predecessor of the key K reduces to two cases: | |||
1. The node X has a left subtree. In this case, the predecessor node is the node with the maximum key in the left subtree, which can be compute with <code>MAXIMUM(left_child(X))</code>, and it is the rightmost leaf. | |||
2. The node X has no left subtree. In this case, the predecessor node is found by walking up in the tree until we find an [[Tree_Concepts#Ancestors_and_Descendants|ancestor]] node with a key smaller than K. It is possible to not find a predecessor, if the node we start with is the minimum in the tree. | |||
==<tt>SUCCESSOR</tt> Implementation== | |||
<font color=darkkhaki>TODO</font> | |||
==<tt>SELECT</tt> Implementation== | |||
To implement <tt>SELECT</tt> efficiently, we need to [[Data_Structures#Augmenting_a_Data_Structure|augment]] the binary tree structure by storing extra information about the tree itself in each tree node. In this specific case, we maintain a "size" field (size(X)) which contains the number of tree nodes that exist in subtree rooted at X. | |||
<font size=-1> | |||
Start at root X with children Y and Z. | |||
Let a = size(Y) <font color=teal># a = 0 if X has no left child</font> | |||
if a = i - 1 return X's key | |||
if a ≥ i recursively compute i<sup>th</sup> order statistic of the search tree rooted at Y | |||
if a < i - 1 recursively compute (i - a - 1)<sup>th</sup> order statistic of the search tree rooted at Z | |||
</font> | |||
The running time is O(tree_height). | |||
Also see: {{Internal|Selection_Problem#Randomized_Selection|Randomized Selection in an Unsorted Array}} | |||
==<tt>RANK</tt> Implementation== | |||
=Balanced vs. Unbalanced Binary Search Trees= | =Balanced vs. Unbalanced Binary Search Trees= | ||
Revision as of 04:03, 13 October 2021
External
- https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/juAOg/balanced-search-trees-operations-and-applications
- https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/1FBl2/binary-search-tree-basics-part-i
- https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/cXMbA/binary-search-tree-basics-part-ii
Internal
Overview
A binary search tree is a binary tree that has the Binary Search Tree Property. It supports insertion, deletions and searches and can be thought as the dynamic version of a sorted array: any operation exposed by a static sorted array is available, but additionally, we have access to insertion and deletion.
While in general the running time of the insertion, deletion and search operations on a binary search tree is asymptotically bounded by the height of the tree, these operations become efficient when the binary search tree is kept balanced, and thus its height is the minimum possible. Balanced binary search trees are addressed in detail below.
A binary search tree is represented in memory using three pointers: left child, right child and the parent. More details on binary tree representation in memory are available here:
Binary Search Tree Property
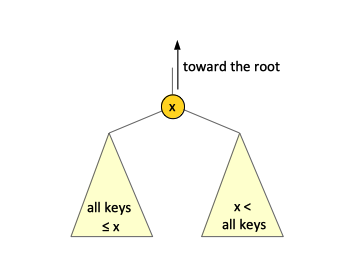
The fundamental property of the binary search tree, called the Binary Search Tree Property:
For every single node of a binary search tree, if the node has a key value, then all of the keys stored in the left subtree should be less than the node's key value and all of the keys stored in the right subtree should be bigger than the node's key value. This property holds not only at the root, but in every single node of the three.
Note that the Binary Search Tree Property is different from the Heap Property. Search tree are designed so we can search easily through them, unlike heaps that are designed to find the minimum (or maximum) easily.
TODO CLRS Page 286.
Supported Operations
| Operation | Running Time | Notes |
|---|---|---|
| INSERT(X) | O(log n) | INSERT Implementation |
| DELETE(X) | O(log n) | DELETE Implementation |
| SEARCH(K) | O(log n) | SEARCH Implementation |
| SELECT(ith order statistics) | O(log n) | SELECT Implementation |
| MINIMUM() | O(log n) | MINIMUM Implementation |
| MAXIMUM() | O(log n) | MAXIMUM Implementation |
| PREDECESSOR(X) | O(log n) | PREDECESSOR Implementation |
| SUCCESSOR(X) | O(log n) | SUCCESSOR Implementation |
| RANK(X) | O(log n) | RANK Implementation |
SEARCH Implementation
SEARCH(root, X)
SEARCH(n, X)
if X == value(n) return n
if X < value(n)
if there is no left child return NULL
else SEARCH(left_child(n), X)
if X > value(n)
if there is no right child return NULL
else SEARCH(right_child(n), X)
The running time is Θ(tree_height).
INSERT Implementation
One implementation, that does not care about keeping the tree balanced, uses the recursive search procedure described above to keep searching for the key to be inserted until a NULL child pointer is encountered. At that point, the procedure wires a new tree node in that position:
INSERT(root, X)
INSERT(n, X)
if X <= value(n)
if there is no left child wire X as left child
else INSERT(left_child(n), X)
if X > value(n)
if there is no right child wire X as right child
else INSERT(right_child(n), X)
The running time is Θ(tree_height).
DELETE Implementation
The DELETE(X) function gets as argument the node to delete. The DELETE(K) function gets as argument the key to delete and in this case we need to locate the node X corresponding to the given key K with SEARCH(K). If no such node exists, nothing is deleted.
To continue, we assume the node X exists.
There are three distinct cases that need to be handled:
1. X has no children. This is the easiest case, the node is just simply deleted from the three.
2. X has just one child - a left child or a right child. In this case, splice out the node to delete, which creates a hole in the tree, and then rewire its child into its parent. The unique child assumes the position of the deleted node.
3. X has both the left and right child. Find the predecessor of the node to be deleted using the PREDECESSOR() function. Since X has both left and right subtrees, the predecessor will be the rightmost leaf of its left subtree, as explained in PREDECESSOR Implementation. Then splice out the node to be deleted and wire the predecessor such found in its place. If the predecessor node has a left child, you may need to wire it into its parent.
MINIMUM Implementation
Search for -∞: Start with the root and follow the left child until the leftmost leaf. The running time is Θ(tree_height).
MAXIMUM Implementation
Search for +∞: Start with the root and follow the right child until the rightmost leaf. The running time is Θ(tree_height).
PREDECESSOR Implementation
Computing the predecessor of a node X in a binary search tree involves finding the node whose key is the next smaller element relative to the X's key.
If the argument to the PREDECESSOR() function is the key itself, the implementation first must search the tree and find the corresponding node. If no node is found, the problem has no solution.
To continue, we assume that the node corresponding to the given key K is found in the tree, and it is X. Computing the predecessor of the key K reduces to two cases:
1. The node X has a left subtree. In this case, the predecessor node is the node with the maximum key in the left subtree, which can be compute with MAXIMUM(left_child(X)), and it is the rightmost leaf.
2. The node X has no left subtree. In this case, the predecessor node is found by walking up in the tree until we find an ancestor node with a key smaller than K. It is possible to not find a predecessor, if the node we start with is the minimum in the tree.
SUCCESSOR Implementation
TODO
SELECT Implementation
To implement SELECT efficiently, we need to augment the binary tree structure by storing extra information about the tree itself in each tree node. In this specific case, we maintain a "size" field (size(X)) which contains the number of tree nodes that exist in subtree rooted at X.
Start at root X with children Y and Z. Let a = size(Y) # a = 0 if X has no left child if a = i - 1 return X's key if a ≥ i recursively compute ith order statistic of the search tree rooted at Y if a < i - 1 recursively compute (i - a - 1)th order statistic of the search tree rooted at Z
The running time is O(tree_height).
Also see:
RANK Implementation
Balanced vs. Unbalanced Binary Search Trees
A binary search tree can be unbalanced or balanced. For the same set of key, the search tree can vary in height between log n and n, where n is the number of keys. Balanced trees are more useful for search because they yield better running times, so techniques to keep the tree balanced while inserting or deleting nodes have been developed.
Balanced Binary Search Tree
The reason to exist for balanced binary search trees is to expose the same set of operations as a static sorted array, while allowing dynamic insertion and deletions. Some of the operations won't be as fast as in the case of a static sorted array, though.