Breadth-First Search-based Shortest Path Algorithm: Difference between revisions
| Line 8: | Line 8: | ||
⚠️ Only breadth-first search gives the guarantee of the shortest path, depth-first search will not provide this guarantee. | ⚠️ Only breadth-first search gives the guarantee of the shortest path, depth-first search will not provide this guarantee. | ||
=Algorithm= | |||
The algorithm is (differences to the [[Graph_Search#BFS_Algorithm_Pseudocode|canonical BFS]] algorithm are emphasized): | |||
<font size=-1> | |||
BFS_with_Shortest_Path(graph G, start vertex s) | |||
<font color=teal># All nodes are assumed unexplored</font> | |||
<font color=SlateGray>initialize a Queue Q (FIFO) | |||
mark s as explored</font> | |||
annotate s with distance 0 | |||
<font color=SlateGray>place s in Q | |||
while Q has elements | |||
remove the head of the queue v | |||
for each edge (v, w): | |||
if w unexplored: | |||
mark w as explored</font> | |||
annotate w with a distance dist(w) = dist(v) + 1 | |||
<font color=SlateGray>add w to Q</font> | |||
</font> | |||
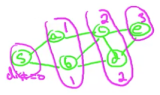
The distance computed on reachable node gives the "layer" and the distance from the start node s. | |||
:::[[File:BFS_Layers.png|160px]] | |||
Revision as of 19:19, 14 October 2021
Internal
Overview
The BFS-based algorithm as described above can be used, with a very small constant-time addition, to keep track of the layer of each newly discovered node, relative to the start node, and that will automatically indicate the shortest path between the start node s and a reachable node v. It works by annotating the start vertex with 0 and then annotating each new node with D + 1, where D is the distance of the node we discovered the new node from.
The BFS-based shortest path algorithm works with both directed and undirected graphs.
⚠️ Only breadth-first search gives the guarantee of the shortest path, depth-first search will not provide this guarantee.
Algorithm
The algorithm is (differences to the canonical BFS algorithm are emphasized):
BFS_with_Shortest_Path(graph G, start vertex s)
# All nodes are assumed unexplored
initialize a Queue Q (FIFO)
mark s as explored
annotate s with distance 0
place s in Q
while Q has elements
remove the head of the queue v
for each edge (v, w):
if w unexplored:
mark w as explored
annotate w with a distance dist(w) = dist(v) + 1
add w to Q
The distance computed on reachable node gives the "layer" and the distance from the start node s.