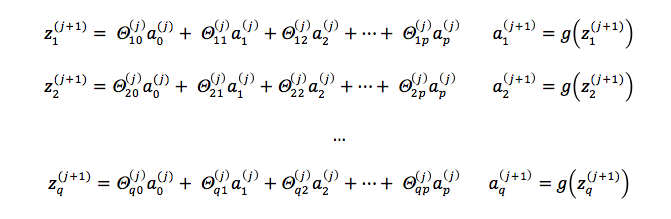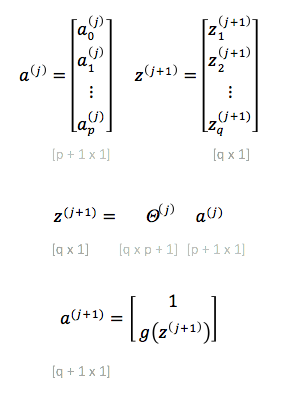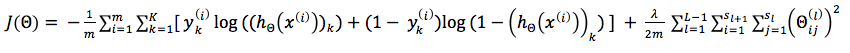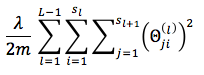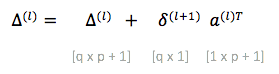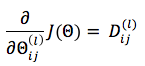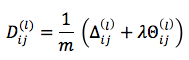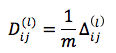Neural Networks

Internal

• Machine Learning

Overview

A neural network consists of several layers of activation units ("individual neurons"), where one layer's activation unit output is connected to the inputs of all activation units of the successive layer. The behavior of an individual activation unit is described here.

Individual Unit

Individual neural network units are computational units that read input features, represented as an unidimensional vector x₁ ... x_n in the diagram below, and calculate the hypothesis function as output of the unit. Note that x₀ is not part of the feature vector, but it represents a bias value for the unit. The output value of the hypothesis function is also called the "activation" of the unit.

A common option is to use a logistic function as hypothesis, thus the unit is referred to as a logistic unit with a sigmoid (logistic) activation function.

The θ vector represents the model's parameters (model's weights). For a multi-layer neural network, the model parameters are collected in matrices named Θ, which will be describe below.

The x0 input node is called the bias unit, and it is optional. When provided, it is equal with 1.

A single activation unit has a function identical to, and works similarly with logistic regression, but instead of applying the logistic function only to a set of input features, it is applied successively to the input features and to activation values of intermediate layers. The intuition behind this behavior is that a neural network gets to learn its own internal features, often across several layers, instead of being constrained to process the input features and immediately produce a result. Practice shows that the network may learn interesting and complex features, which can lead to a better hypothesis.

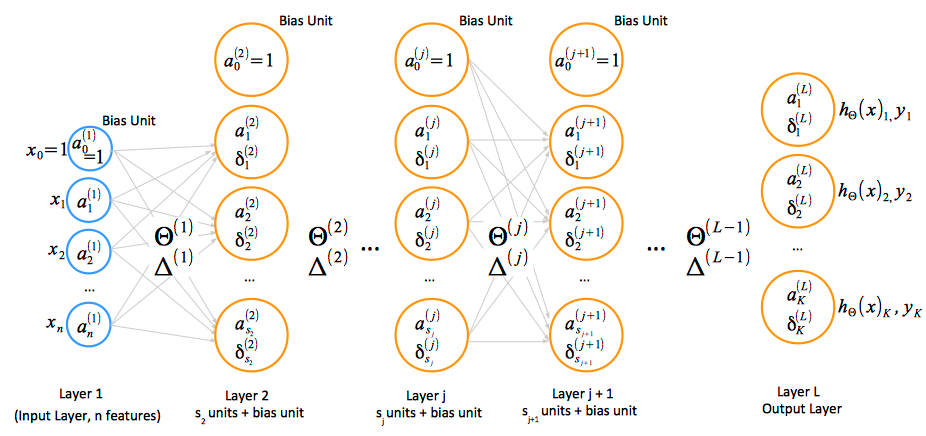
Multi-Layer Neural Network

Notations and Conventions

activation: a_i^(j) represents the "activation" of unit i in layer j. The input values x can be thought of as the activations of the input layer, conventionally named layer 1, and so they can be consistently named a₁⁽¹⁾, a₂⁽¹⁾, ... a_n⁽¹⁾. The input bias unit is a₀⁽¹⁾=1.

parameter matrix Θ: Θ^(j) represents the matrix of parameters (weights) that controls function mapping from layer j to layer j + 1.

the total number of layers in the network is conventionally named L.

the number of units in the layer l is conventionally named s_l. This number does not include the bias unit.

the total number of classes - which is the same as the total number of output until, is named K.

forward propagation: A vectorized implementation of the forward propagation algorithm is available in the "Layer j + 1 Forward Propagation Vectorized Implementation" section.

backpropagation: the algorithm for minimization of a neural network cost function. More details are available in the "Backpropagation section below.

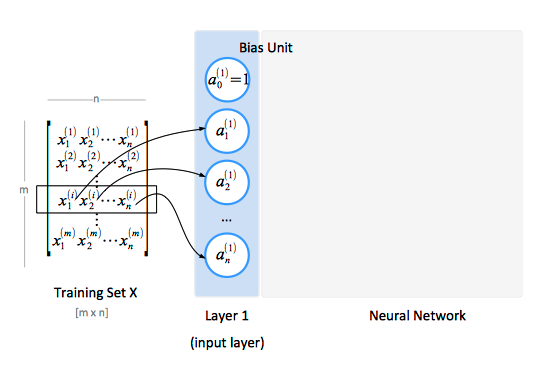
The Input Layer

The input layer, conventionally named "layer 1", consists of input nodes. The input layer provides the training values. A training set contains a number of samples (m), and each sample has a number of features (n). The features of the training set are conventionally represented as a matrix X.

The Hidden Layers

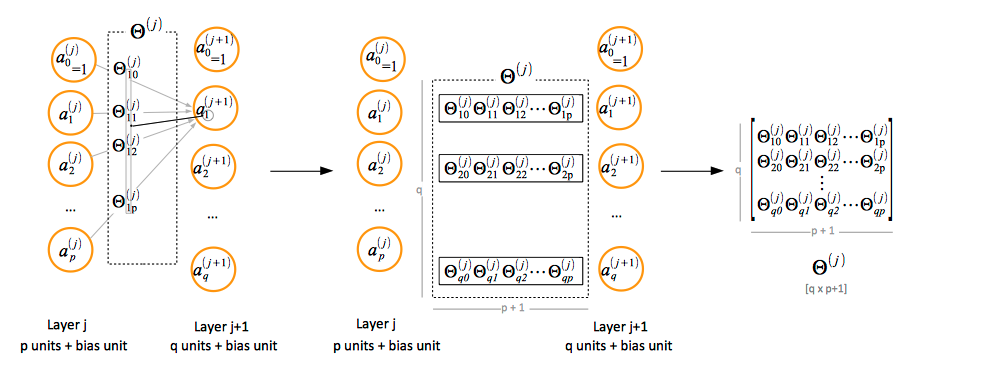
Paramenter Matrix Θ Notation Convention

If the layer j has p units, not counting the bias unit, and layer j + 1 has q units, not counting the bias unit, then the parameter matrix Θ^(j) controlling function mapping from layer j to layer j + 1 has q x (p + 1) elements. The "+1" comes from the addition of the bias node in layer j.

Layer j + 1 Unit Activation Values

In order to compute the activation values of a layer j + 1, we calculate the weighted linear combination of the input values (or the activation values of the previous layer), conventionally named z_i^{(j + 1)} and then we apply the logistic function to the result.

Layer j + 1 Forward Propagation Vectorized Implementation

To obtain the activation values of the output layer, we don't need to add the bias unit to the result vector.

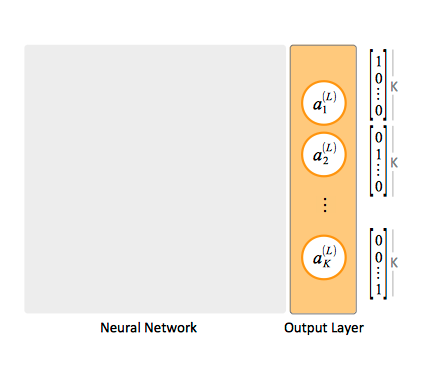
The Output Layer

For multi-class classification, the training set's each y value is represented as a vector containing binary values.

When an element of a specific class is matched, the corresponding unit in the output layer will product an activation value of 1, while all other units produce a 0 activation value. The output layer has as many units as classes we are attempting to classify.

Neural Network Training

The following steps describe the procedure of the neural network training, otherwise known as "fitting the parameters".

The procedure has the objective of minimizing the network's cost function: given the cost function J(Θ), we want to find parameters Θ that minimize J(Θ).

An advanced minimization algorithm can do that if we provide J(Θ) and partial derivatives. The code that calculates J(Θ) is based on the formula provided in the "Regularized Cost Function" section. The partial derivative values are computed via backpropagation.

Regularized Cost Function

The cost function for a multi-class neural network is a generalization of the logistic regression regularized cost function, as follows:

where the double sum adds the logistic regression regularized cost function over each of the K output units, and then adds the result over the entire length of the training set. In this expression, (h_Θ(x))_k represents the k^th element of the output vector.

The regularization term sums all the squared values of all Θ matrices, except the terms corresponding to the bias values. The i index in this sum does not refer to the index of the row in the training set.

Note that the regularization term is sometimes computing using the following formula, which yields the same result:

The MATLAB function that computes the regularization term for an individual Θ matrix:

function rt = regularizationTerm(lambda, m, Theta)

% We expect that the weights corresponding to the bias values
% are provided on the first column of the Theta matrix, so we
% drop them

if lambda == 0
    rt = 0;
else
    columns = size(Theta, 2);
    T = Theta(:, 2: columns);
    rt = (lambda / (2 * m)) * sum(sum(T .^ 2));
end
end

Weight Initialization

Weights should be initialized randomly to avoid the problem of symmetric ways.

Forward Propagation

Implement forward propagation to get h_Θ(x⁽ⁱ⁾) for any x⁽ⁱ⁾ of the training set. This is done by assigning input (x⁽ⁱ⁾) to to layer 1, and then steping from left to right through layers, calculating unit activation values for layers 2, 3 ... L using the formulae described in the "Layer j + 1 Unit Activation Values" and "Layer j + 1 Forward Propagation Vectorized Implementation" sections.

Backpropagation

The backpropagation algorithm computes the partial derivatives of the cost function over Θ_jk^(l).

It does that by forward propagating a training set sample though the network, until it obtains the hypothesis function values for the current matrix of parameters, then it reverse course, starting with comparing the hypothesis function values with the actual values coming from the training set, computing the "errors" between the expected result and calculated result, and backpropagating those errors into the network. Backpropagation is mathematically similar to forward propagation, except that the computations are flowing from the left to the right of the network.

The algorithm calculates an "error term" value δ_j^(l) for each node of the network. The value represents the "error" in the activation value a_j^(l) of the node j in layer l. The error values thus calculated are used in computing the partial derivatives of the cost function over each Θ element, for each relevant layer of the network.

The partial derivatives, together with the cost function J(Θ) are used by a gradient descent algorithm, or by other advanced minimization algorithms to minimize the cost function.

The algorithm starts with calculating the error at the output layer, as the difference between our network's results and the actual values coming from the training set:

It then steps back from right to left through layers, calculating unit errors δ^(L-1), δ^(L-2), ... δ⁽²⁾ as follows:

The delta values in layer j are calculated multiplying the transposed Θ^(j) [p + 1 x q] for the layer with the vector [q x 1] containing delta values of the j + 1 layer to its right, and then doing element-wise multiplication with the derivative of the activation function g() evaluated with the input values given by z^(j). It can be demonstrated that:

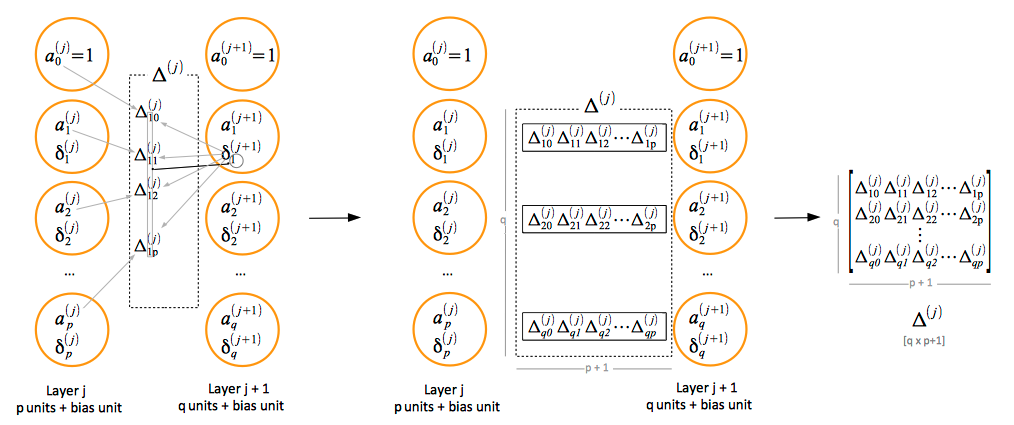
The resulted δ^(j) is a [p + 1 x 1] vector. The error terms thus calculated are further used to calculate the gradient for this specific sample, and accumulate it in the Δ^(j) matrix. This is done by dropping the error term corresponding to the bias unit δ₀^(j) and applying the following operation:

Mathematically, each element of the error matrix Δ that controls error backpropagation between layer j and j + 1 is calculated as follows:

The errors accumulate with iterations over the training set as follows:

The corresponding vectorized expression is:

The partial derivative of the cost function J(Θ) over the elements of the Θ matrix is given by the formula:

where:

• if j is not 0.
• if j is 0.