Heap
External
- https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/iIzo8/heaps-operations-and-applications
- https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/KKqlm/heaps-implementation-details-advanced-optional
Internal
Overview
This article is about binary heaps. A binary heap data structure is an array where data is placed to form a complete binary tree, plus the index of the last node in the heap. Each element of the array contains a pointer to tree nodes. Each node contains at least a key. The heap works by comparing key and placing the pointer of the associated nodes in the right position in the heap. Duplicate key values are supported. For more details on representation in memory, see the Representation in Memory section below.
The heap data structure maintains an invariant, called the heap property.
Another name used for heaps are priority queues.
More details CLRS page 151, page 1177.
The Heap Property
For every node x, key[x] ≤ all keys of its children.
Canonical Uses of a Heap
The primary reason to use a heap is if you notice that your program does repeated minimum (maximum) computations, usually via exhaustive search.
Also see:
Supported Operations
INSERT
Insert a node in the tree. The running time is O(log n) where n is the number of nodes. For implementation, see INSERT Implementation below.
Also see:
REMOVE-MIN
Remove the node from the heap with minimum key value. The running time is O(log n) where n is the number of nodes. For implementation see REMOVE-MIN Implementation below.
Also see:
Min Heap and Max Heap
A heap is constructed in such a way that it maintains a minimum value or a maximum value, but not both. A heap that maintains the minimum value is called a min heap and supports the REMOVE-MIN operation. A heap that maintains the maximum value is called a max heap and supports the REMOVE-MAX operation. If both extracting minimum and maximum are required, use a binary search tree instead.
HEAPIFY
Initialize the heap in linear time O(n). Using INSERT would take O(n log n), but HEAPIFY does it in O(n) when invoked on a batch of n elements.
DELETE
Delete an arbitrary node in the middle of the heap in O(log n) time. This is useful when implementing Dijkstra's Algorithm
Also see:
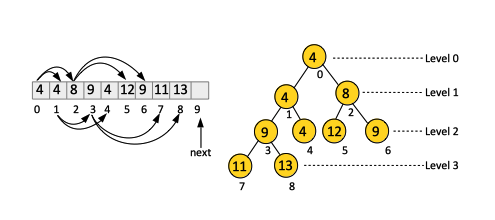
Representation in Memory
A heap has two conceptual representations: one is a rooted binary tree, as complete as possible, and the other one is an array.
For each node i, the left children is maintained at 2i+1 and the right children is maintained at 2i + 2.
Conversely, for a node i, the parent is maintained at ⌊i/2⌋.
The advantage of the heap array representation is that rather than traversing pointers, it is very fast to just go from a node to its parent or to either one of its children by doing index arithmetic with bit shifting. Also, we don't need the overhead of storing references.
The fact that the binary tree is as complete as possible (the nodes are added layer by layer, and left to right) is essential for the heap array representation.