Binary Search Trees

External

• https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/juAOg/balanced-search-trees-operations-and-applications
• https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/1FBl2/binary-search-tree-basics-part-i
• https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/cXMbA/binary-search-tree-basics-part-ii

Internal

• Tree Concepts

Overview

A binary search tree is a binary tree that has the Binary Search Tree Property. It supports insertion, deletions and searches and can be thought as the dynamic version of a sorted array: any operation exposed by a static sorted array is available, but additionally, we have access to insertion and deletion.

While in general the running time of the insertion, deletion and search operations on a binary search tree is asymptotically bounded by the height of the tree, these operations become efficient when the binary search tree is kept balanced, and thus its height is the minimum possible. Balanced binary search trees are addressed in detail below.

A binary search tree is represented in memory using three pointers: left child, right child and the parent. More details on binary tree representation in memory are available here:

Binary Tree Representation in Memory

Binary Search Tree Property

The fundamental property of the binary search tree, called the Binary Search Tree Property:

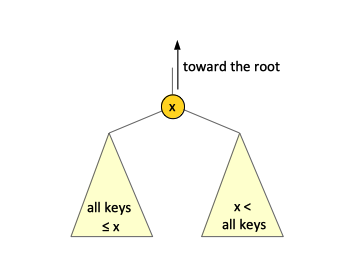
For every single node of a binary search tree, if the node has a key value, then all of the keys stored in the left subtree should be less than the node's key value and all of the keys stored in the right subtree should be bigger than the node's key value. This property holds not only at the root, but in every single node of the three.

Note that the Binary Search Tree Property is different from the Heap Property. Search tree are designed so we can search easily through them, unlike heaps that are designed to find the minimum (or maximum) easily.

TODO CLRS Page 286.

Balanced vs. Unbalanced Binary Search Trees

A binary search tree can be unbalanced or balanced. For the same set of key, the search tree can vary in height between log n and n, where n is the number of keys. Balanced trees are more useful for search because they yield better running times, so techniques to keep the tree balanced while inserting or deleting nodes have been developed.