Binary Codes
External
- https://www.coursera.org/learn/algorithms-greedy/lecture/plgXS/introduction-and-motivation
- https://www.coursera.org/learn/algorithms-greedy/lecture/IWxVe/problem-definition
Internal
Overview
A binary code is a function that maps each symbol (character) of an alphabet Σ to a binary string. When the binary representation of each character of the alphabet has the same length, the code is said to be a fixed length code. The alternative is a variable length code.
Binary Encoding as Binary Tree
In general, any binary code can be expressed as a binary tree with the left child edges labeled with 0, right child edges labeled with 1 and leaves labeled with the symbols of the alphabet. The tree also contain internal nodes that are not labeled. The bits from the root down to the leaf labeled with a given symbol correspond to the proposed encoding for that symbol. A benefit of representing a code as a tree is that it gives a very natural representation of decoding: start at the root of the tree and for a 0 go left, and for a 1 go right. Once you encounter a leaf, and that leaf carries the symbol that was encoded.
Depth
Encoding lengths of the symbols - the number of bits needed to encode various symbols - are the depths of the corresponding leaves in the tree.
Fixed Length Code
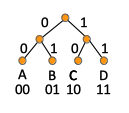
A fixed length binary code is a binary code that maps each character of the alphabet Σ to a fixed length representation. Arbitrary characters have the same length representation in the binary code. An example of fixed length code for the alphabet Σ = {A, B, C, D} is {00, 01, 10, 11}, where we use 2 bits per each character. If we think about the binary code as a binary tree, the representation of this fixed length encoding is:
ASCII is a well known example of a fixed length binary code.
However, in the case when some characters are more likely to appear than others, a schema that allocates shorter codes to characters that are likely to appear more frequently tends to encode information using fewer bits. This encoding schemas are called variable length codes.
Variable Length Code
A variable length binary code is a binary code that maps each character of the alphabet Σ to a variable length representation, usually in relation to the frequency the character is used in certain patterns of communication. The more frequent characters are associated with shorter variable length codes, resulting in shorter encodings. A Huffman code is an example of variable length binary code.
A problem with variable length codes is that they may introduce ambiguity that makes decoding problematic. For example, in the case of the alphabet Σ = {A, B, C, D}, if we use the encoding {0, 1, 01, 10}, there is not enough information to decode 001. It could be decoded as AAB or as AC, because without further precautions, it is not clear when one symbol ends and another symbol begins. In case of a binary tree representation, this is a situation where an internal node represents one characters of the alphabet, while there are descendants of that node that also represent characters of the alphabet. When this happens, there is not enough information to know when to stop. This problem is solved with prefix-free codes.
Producing an efficient variable length code requires a priori domain knowledge, where we know the relative frequency of the alphabet symbols. For example, the usual frequency for A, C, G and Ts are known in genomics. In the case of MP3 encoding, we can take an intermediate version of the file after analog-to-digital conversion and count the occurrences of each of the symbols.
Prefix-Free Codes
Prefix-free codes solve the ambiguity of decoding variable length code-encoded content.
A prefix-free code is defined as follows: for every pair i,j of characters in the alphabet Σ, neither of the encodings f(i) and f(j) is a prefix of the other.
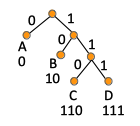
In the previous example, the {0, 1, 01, 10} encoding of the alphabet Σ = {A, B, C, D} is not prefix free, as A and C encodings have the same prefix, and also B and D. However, {0, 10, 110, 111} is a prefix free encoding. If we represent a prefix-free encoding as a binary tree, the tree nodes are associated with characters only for the leaves of the tree. The tree is not balanced.
The befit of thinking about prefix-code as trees is that the prefix-free condition shows up in a clean way, namely the prefix-free condition is the same as leaves being the only nodes that have character labels. No internal nodes are allowed to have a label in a prefix-free code. The code of a character is given by the bits along paths from root to the labeled node, and since all labeled nodes are leaves, no path of a node is the prefix of the other. For a node to have a code that is a prefix to other node's code is to be the ancestor of the other node in the tree, and since all nodes are leaves, no node is the ancestor of other node.
The Optimal Variable-Length Binary Code Problem
Given characters from an alphabet Σ with a priory known probability pi for each character i ∈ Σ, minimize average encoding length.
The average encoding length is expressed as the average depth of each character in the encoding binary tree T, weighted by its probability pi:
L(T) = ∑ pi*[depth of i in T] i∈Σ
The L(T) is the objective function we want to minimize. The solution of the problem should be the binary tree whose leaves are annotated with symbols of Σ. The paths from roots to symbols are the actual optimal codes. The Huffman algorithm presented below, provides an optimal solution to this problem.
The Huffman Algorithm
The Huffman algorithm is a recursive greedy algorithm that constructs the prefix-free variable length binary code for a given alphabet and associated character probabilities, in such a way that it minimize the average encoding length. The problem is formally described above.
The idea is to start with all the individual characters of the alphabet, as unconnected leaves of the tree, and then perform successive mergers, fusing the leaves bottom-up into subtrees under common internal nodes, until eventually all sub-trees coalesce into the optimal encoding tree. We always merge the two symbols with the smallest frequencies in the alphabet. This is the greedy criterion of the greedy algorithm, and the intuition behind this choice is explained below. The merged symbols become a new symbol in a new, smaller alphabet Σ'. The probability of the new symbol is the sum of the probabilities of the symbols that were combined. The algorithm is repeated recursively until we have a two-symbol alphabet, which represents the base case.
When we merge two subtrees, each containing a collection of symbols as leaves, we introduce a new internal node which unites these two subtrees under it. This internal node will become yet another internal node on the path from root to a leaf, for all the leaves in these subtrees. The final encoding length of a symbol is precisely the number of mergers its subtrees have to endure. Every time a subtree is merged, its symbols pick up one extra bit in their encoding. This is the reason we start to merge the symbols with the lowest probability, because we want to minimize the average encoding length weighted by probability, and since the encoding length is going to be long for the symbols we start with, we choose those with the lowest probability - the least unhappy to suffer an increment to their encoding length.
if │Σ│ = 2 return a subtree with two leaves and an intermediary node Choose a,b ∈ Σ that have the smallest frequencies Let Σ' = Σ with a,b replaced by a new symbol ab Define pab = pa + pb Recursively compute T' # for the alphabet Σ' Extend T' to a tree T with leaves in Σ by splitting the leaf ab into two leaves a and b Return T