Graph Concepts
Internal
Graph Definition
A graph is a pair-wise relationship among a set of objects. Mathematically, a graph G is a pair (V, E), where V is a finite set of vertices, called the vertex set of G, and E is a binary relation on G, called the edge set of G. The edge set contains the graph's edges.
n and m Convention
The convention used in graph algorithms is to denote the number of vertices with n and the number of edges with m. In most, but not all, applications, m is Ω(n) and O(n2). Also see sparse graphs and dense graphs.
Vertices and Edges
Vertex (Node)
An elements of the vertex set V is called vertex, plural vertices. A vertex has zero or more edges associated with it. An alternate term for vertex, used sometimes in the graph theory literature, is node. We prefer to use the term "node" when we refer to the vertices of rooted trees. We use "vertex" as a more generic term that refers to graphs in general. Another alternate name is entity.
Source Vertex
Some algorithms, as for example the algorithms that compute the shortest path in a graph need a vertex to start from. That vertex is usually called the source vertex or the starting vertex.
Edge (Arc)
The elements of the edge set E are called edges, also known as relationships or arcs. By convention, we use (u, v) notation for an edge, where u and v represent vertices in V. The order in which vertices are specified for an edge may be relevant. If the order in which the vertices are specified matters, then the graph is a directed graph. If the order in which the vertices are specified does not matter, then the graph is an undirected graph.
For undirected graphs, edges are said to be incident on vertices, while for directed graphs, edges can be incident to and from vertices.
Parallel Arcs
Two parallel arcs (or parallel edges) are two arcs that have the same vertices.
Self-Loops
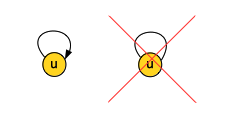
A self-loop is an edge incident from and incident to the same vertex. Self loops are only allowed in directed graphs.
Edge Length
Conventionally, the length of an edge is represented using ℓe notation. The terms "edge length" and "edge weight" are used interchangeably, and this is where the term weighted graph comes from. Yet another term for edge length is edge cost, represented using the ce notation, and this term is at the origin of the cost of a subgraph or cost of a spanning three.
Negative Length Edge
Dijkstra's shortest-path algorithm cannot compute the shortest path correctly in presence of negative length edges. Bellman-Ford shortest-path algorithm can.
Vertex Adjacency
If (u, v) is an edge in a graph G = (V, E), we say that the vertex v is adjacent to vertex u. In other words, if two vertices have an edge connecting them, they are adjacent. For undirected graphs, the adjacency relation is symmetric: if vertex u is adjacent to vertex v, then automatically vertex v is adjacent to vertex u. This is not the case for directed graphs: u → v ≠ v → u, which says that for directed graphs the adjacency relation is not symmetric.
Independent Set
An independent set of a graph is a subset of the graph's vertices so that no two vertices are adjacent.
Vertex Degree
The vertex degree is the count of edges incident on, from and to the vertex, depending on the type of the graph.
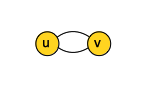
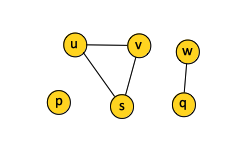
For undirected graphs, the vertex degree is the number of edges incident on the vertex, which is the same with the number of adjacent vertices. In the example below, the vertex v has degree 2.
For an undirected graphs, the following relationship holds true:
∑ degree(v) = 2m v
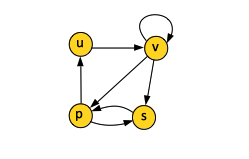
For directed graphs, we define the in-degree as the number of edges entering the vertex and the out-degree as the number of edges exiting the vertex. The degree of the vertex is the sum of in-degree and out-degree. In the example above, vertex v has an in-degree 2, out-degree 3 and degree 5.
Graph Directionality
Undirected Graph
An undirected graph is a (V, E) pair where the edge set E contains undirected edges: the order in which the vertices are specified when the edge is defined does not matter and (u, v) is equivalent with (v, u) - they are considered to be the same edge. Another way to define an unordered graph is that its edges are sets {u, v} where u, v ∈ V and u ≠ v.
⚠️ Self-loops are not allowed in an undirected graph. Every edge is incident on two distinct vertices.
If (u, v) is an edge in an undirected graph G = (V, E), we say that (u, v) is incident on both vertices u and v. In the example above, edges incidents on vertex v are (u, v) and (v, s).
An undirected graph in which each pair of vertices is adjacent is called a complete graph.
Tree
A tree is a connected, acyclic, undirected graph. A tree defined as such is sometimes referred to as a free tree. More details about trees are available in the Tree Concepts section.
Forest
A forest is an acyclic, undirected graph. Note that the graph may be disconnected - may consists in several disconnected trees.
Directed Graph
A directed graph is a (V, E) pair where the edge set E contains directed edges: the order in which the vertices are specified when the edge is defined matters. For a directed graph, (u, v) and (v, u) are distinct edges. That is why we sometimes write the edge as u → v and v → u.
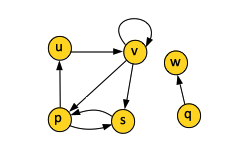
A characteristic of a directed graph is that self-loops, edges from a vertex to itself, are allowed. A self-loop is a cycle of length 1.
A directed graph with no self-loops is simple.
Edge Incident From Tail Vertex
If (u, v) is an edge in a directed graph G = (V, E), we say that (u, v) (u → v) is incident from, or leaves vertex u. The vertex u is referred to as the tail vertex. In the example above, edges (v, v), (v, p) and (v, s) leave tail vertex v.
Edge Incident To Head Vertex
If (u, v) is an edge in a directed graph G = (V, E), we say that (u, v) (u → v) is incident to, or enters, vertex v. The vertex v is referred to as the head vertex. In the example above, edges (v, v) and (u, v) enter head vertex v.
TODO: https://www.cs.princeton.edu/courses/archive/spr03/cs226/lectures/digraph.4up.pdf
Topological Order of a Directed Graph
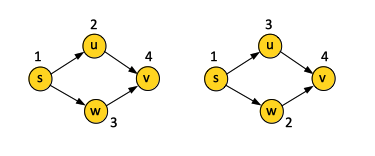
A topological order of a directed graph G is a function (labeling) f of G's nodes such that:
- the values of f(v) are the set {1, 2, ..., n}
- (u, v) ∈ G ⇒ f(u) < f(v)
An intuitive interpretation of the topological order is that all edges go "forward" when we place the nodes in a line.
A directed graph has a topological ordering only if it is acyclic, or a directed acyclic graph (DAG). If the directed graph has a directed cycle, there cannot be a topological ordering of that graph. On the other hand, if a directed graph has no directed cycles, this condition is strong enough to guarantee that a topological order can be computed - the graph can be topologically sorted.
Also see:
Directed Graphs and Cycles
See Directed Graph Cycles below.
Graph Density
Sparse Graphs
A sparse graph is a graph for which │E│ is much smaller than │V│2. Otherwise said, for a sparse graph m is O(n) or close to it. Sparse graphs are usually represented as adjacency lists in memory.
Dense Graphs
A dense graph is a graph for which │E│ is close to │V│2. Otherwise said, for a dense graph m is closer to O(n2). Dense graphs are usually represented as adjacency matrices in memory.
Paths
A path of length k from a vertex u to a vertex u' in a graph G = (V, E) is a sequence (v0, v1, ..., vk) of vertices such that u = v0, u' = vk and the edge (vi-1, vi) ∈ E for i = 1, 2, ... k. Some sources refer to a path as a "walk".
We say that the path contains the vertices v0, ..., vk and the edges (v0, v1), (v1, v2), ..., (vk-1, vk).
If there is a path p from u to u', we say that u' is reachable from u via path p.
A path is simple if all vertices in it are distinct. In the directed graph example above, the path (u, v, p, s) is a simple path of length 3. The path (v, p, s, p) is not simple.
A subpath of a path p = (v0, v1, ..., vk) is a contiguous subsequence of its vertices: for any 0 ≤ i ≤ j ≤ k, the subsequence of vertices (vi, vi+1, ..., vj) is a subpath.
Path Length
The length of the path is the number of edges in the path. The number of vertices is the path length plus one. There is always a zero-length path from u to u. The path lengths is some times referred as path weight or path cost.
In case the edges have explicit lengths ℓe, the length of the path is the sum of the lengths of the individual edges in the path.
Path Graph
Cycles
Undirected Graphs Cycles
For undirected graphs, a path (v0, v1, ..., vk) forms a cycle if k ≥ 3 and v0 = vk. The circle is simple if v1, v2, ..., vk are distinct.
Directed Graphs Cycles
For directed graphs, a path (v0, v1, ... vk) forms a cycle if v0 = vk and the path contains at least one edge. The cycle is simple if, in addition, v1, v2, ... vk are distinct.
A self-loop is a cycle of length 1.
Two paths (v0, v1, ...., vk-1, v0) and (v'0, v'1, ...., v'k-1, v'0) form the same cycle if there exists an integer j such that v'i = v(i + j) mod k for i = 0, 1, ..., k - 1.
Acyclic Graphs
An acyclic graph is a graph that has no cycles.
Directed Acyclic Graph (DAG)
A directed acyclic graph is a directed graph that has no directed cycles - paths that start from a node, follow the directed edges and return to the same node. It is sometimes abbreviated to DAG. One of the practical applications of DAGs is to model dependencies between entities: a directed edge between vertices u and v u → v means that u is a pre-requisite for v, u needs to happen first, or v depends on u. Directed acyclic graphs have a topological ordering. The depth-first search algorithm can be used to compute the topological sort of a directed acyclic graph:
Sink Vertex
Every directed acyclic graph has one or more sink vertices, which are vertices without any outgoing arcs. A directed graph without a sink vertex must have a cycle, hence is not a directed acyclic graph. The sink vertex concept is useful in the straightforward implementation of the topological sorting algorithm of DAGs.
Graph Distances
Shortest-Path Distance between Two Vertices
The shortest-path distance between s and t is the fewest number of edges in an s-t path.
Diameter
The diameter of a graph is the maximum, over all choices of vertices s and t, of the shortest-path distance between s and t. In other words, the maximum possible shortest-path distance that can be found in the graph. It is represented as D(g).
Radius
A radius exists only if the graph has a diameter. The radius of the graph r(G) is the minimum along all the maximum distances between a vertex to all other vertices.
Formally, for a vertex s, let l(s) denote the maximum, over all vertices, of the shortest-path distances between s an t. r(G) is the minimum of l(s) over all choices of the vertex s.
r(G) ≤ D(G) r(G) ≥ D(G)/2
Connectivity and Graph Components
Undirected Graph Connectivity
An undirected graph is connected if every vertex is reachable from all other vertices. Another way of saying that a graph is connected is that it contains a path from any vertex to any other vertex.
Connected Component
A connected component of a graph is the equivalence class of the relation between vertices u ~ v ⇔ ∃ u-v path in G.
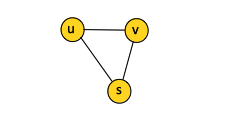
The connected components of a graph are the equivalence classes of vertices under the "is reachable from" relation. The undirected graph example above has three connected components: {u, v, s}, {w, q} and {p}. The edges of a connected component are those that are incident only on the vertices of the component; in other words, the edge (u, v) is an edge of a connected component only if both u and v are vertices of the component.
An entire undirected graph is connected if it has exactly one connected component.
The connected components of an undirected graph can be computed with a breadth-first search-based algorithm:
Directed Graph Connectivity
A directed graph is strongly connected if every two vertices are reachable from each other.
Strongly Connected Component
The strongly connected components (SCC) of a directed graph are the equivalence classes of vertices under are mutually reachable relation.
The formal definition of strongly connected component (SCC) of a directed graph G is the equivalence classes of the relation:
u ~ v ⇔ ∃ a path u → v and
∃ a path v → u in G
Intuitively, a component is strongly connected if we can get from any node to any other node, following directed args. A strongly connected components require cycles.
An entire directed graph is strongly connected if it has only one strongly connected component.
The strongly connected components of a directed graph can be computed with the Kosaraju's depth-first search algorithm:
Directed Graph Connectivity Considerations
Every directed graph has two levels of granularity: the nodes can be clustered in strongly connected components, and those strongly connected components form a DAG.
The following claim can be proven: the strongly connected components of a directed graph induce an acyclic meta-graph. The meta-nodes are the SCCs C1, ... Ck.
Reversing arcs in a directed graph does not affect the strongly connected components, they remain exactly the same.
Graph Cuts
A cut of a graph (V, E) is a partition of V into two non-empty vertex sets A and B.
A ⋃ B = V.
A graph with n vertices has 2n-2 cuts. Why?
Cuts and Edges
Once the A and B are defined, for undirected graph edges fall into three categories: edges with both endpoints in A, edges with both endpoints in B and edges with one endpoint in A and one endpoint in B.
In case of directed graphs, there are directed edges with both endpoints in A, directed edges with both endpoints in B, edges that cross the cut from left to right and edges that cross the cut in the opposite direction.
Crossing Edges
The crossing edges of a cut (A, B) are those with:
- undirected graphs: one endpoint in each of A and B
- directed graphs: tail in A, head in B
Empty Cut Lemma
A graph G is not connected ⇔ ∃ G cut (A, B) with no crossing edges.
The proof is available here.
Empty cut lemma can be used to say when a graph is connected.
Double-Crossing Lemma
Suppose the cycle C ⊆ E has an edge crossing the cut (A, B), then so does some other edge of C.
The double-crossing lemma says that a cycle has an edge crossing the cut, then the cycle has to cross the cut twice.
Lonely Cut Corollary
If e is the only edge crossing some cut (A, B), then it is not in any cycle.
If it were in a cycle, then some other edge would have to cross the cut according to Double-Crossing Lemma.
The Cut Property
Consider an edge e of G. Suppose there is a cut (A, B) such that e is the cheapest edge of G that crosses it. Then e belongs to the minimum spanning tree of G.
If we find just one cut for which a specific edge is the cheapest, that is enough to justify adding the edge to the minimum spanning tree. In the above definition, we specified the MST under the assumption that each edge cost is distinct. In this case there is just one MST. If the edge costs are not distinct, there will be more than one MSTs. The proof of the cut property is available here.
The Minimum Cut Problem
Spanning Trees
A spanning tree of a graph is a subgraph that:
- contains all vertices of the original graph
- contains no cycles (this is what makes it a tree)
The term subgraph comes from the fact that is contains a smaller number of edges, even though it contains the same number of vertices as the spanned graph. There are usually multiple spanning trees for a given graph.
Spanning Tree Cost
The cost of a spanning tree is the sum of the tree's edges costs ce (or lengths).
Minimum Spanning Tree (MST)
A minimum spanning tree is a spanning tree with the minimum cost. If the costs of all edges are distinct, there is guaranteed to be just one MST. If costs are non-distinct, different tie-breaking rules generally yield different spanning trees.
Computing the minimum cost spanning tree for a graph is the subject of the Minimum Spanning Tree Problem and there are several algorithms that compute such trees: Prim's Algorithm, Kruskal's Algorithm. Also see The Cut Property above.
Matching
Given a graph G = (V, E), a matching M in G is a set of pairwise non-adjacent edges, none of which are loops: no two edges share common vertices.
Perfect Matching
A perfect matching is a matching that covers every vertex of a graph.
Formally, given a graph G = (V, E), a perfect matching in G is a subset M of E, such that every vertex in V is adjacent to exactly one edge in M.
Perfect Matching of a Tree
A path with an even number of vertices has a perfect matching:
A path with an odd number of vertices does not have a perfect matching.
Isomorphic Graphs
Two graphs G = (V, E) and G' = (V', E') are isomorphic if there exists a bijection f : V → V' such that (u, v) ∈ E if and only if (f(u), f(v)) ∈ E'. This also can be expressed as follows: we can relabel the vertices of G to be vertices of G', maintaining the corresponding edges in G and G'.
Subgraphs
We say that a graph G' = (V', E') is a subgraph of G = (V, E) if V' ⊆ V and E' ⊆ E.
Given a set V' ⊆ V, the subgraph of G induced by V' is the graph G' = (V', E') where E' = {(u, v) ∈ E: u, v ∈ V'}.
Contraction
The contraction of an undirected graph G = (V, E) by an edge e = (u, v) is a graph G' = (V', E') where V' = V - {u, v} ⋃ {x} and x is a new vertex. The set of edges E' is formed from E by deleting the edge (u, v) and, for each vertex w incident on u or v, deleting whichever of (u, w) and (v, w) is in E and adding the new edge (x, w). In effect, u and v are "contracted" into a single vertex.
Contractions are the base of Karger's minimal cut algorithm.
Weighted Graphs
A weighted graph is a graph where edges have arbitrary, non-unit lengths.