Graph Representation in Memory: Difference between revisions
| Line 31: | Line 31: | ||
Such a structure allows returning head vertices for all directed edges for which a vertex v is the tail in an O(1). | Such a structure allows returning head vertices for all directed edges for which a vertex v is the tail in an O(1). | ||
However, if we need all the tails for which a | However, if we need all the tails for which a given vertex is the head, all adjacency lists must be scanned in an O(m) operation. | ||
=Adjacency Matrices= | =Adjacency Matrices= | ||
Revision as of 04:12, 5 October 2021
Internal
Overview
CLRS page 589, DDIA location 1392.
Graph Input Size
The input size of a graph is given by two parameters: the number of vertices (n) and the number of edges (m). For a connected, undirected graph with n vertices, the number of edges ranges from n - 1 and n⋅(n - 1)/2.
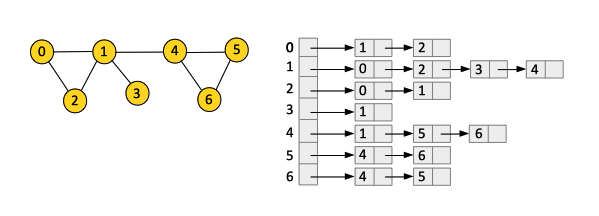
Adjacency Lists
An adjacency list graph is a data structure that keeps track of vertices and edges as independent entities. The structure can be used to store both directed and undirected graphs.
In its most generic form, it has an array or a list of vertices and an array or a list of edges. These two arrays cross-reference each other. Each edge has two pointers, one for each of its vertex endpoints. For directed graphs we keep track of which one is the head and which one is the tail. Each vertex points to all of the edges of which it is a member. For directed graphs, a vertex keeps track of each of the edges it is the tail.
A practical implementation (see CLRS page 590) consists of an array adj of n lists, where the n is the number of vertices. Each array element corresponds to one of the graph's vertices, numbered from 0 to n-1, and contains an adjacency list for that vertex: the list that contains all the vertices in the graph for which there's an edge from the current vertex. That is, adj[i] contains all the vertices adjacent to i in the graph.
The space requirements for this data structure is Θ(n + m). An adjacency list representation provides a memory-efficient way of representing sparse graphs, so it is usually the method of choice. Adjacency lists are very well suited for graph search.
Adjacency Lists and Undirected Graphs
For an undirected graph, the adjacency list for a given vertex v contains all the vertices u for which there is an edge (v, u). Because the edge is undirected, it counts as valid edge for both vertices v and u, so v will also show up in the adjacency list for vertex u. Each edge is represented twice. For a directed graph, that is not the case, as u → v ≠ v → u.
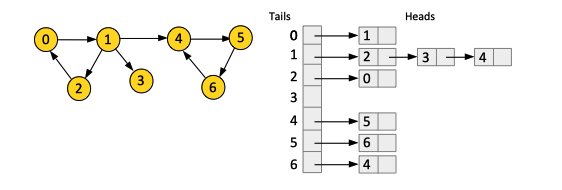
Adjacency Lists and Directed Graphs
For a directed graph, an adjacency list for a vertex v contain all vertices u for which there is a directed edge v → u, incident from v. v is the tail of the edges, and the vertices u are the heads.
Such a structure allows returning head vertices for all directed edges for which a vertex v is the tail in an O(1).
However, if we need all the tails for which a given vertex is the head, all adjacency lists must be scanned in an O(m) operation.
Adjacency Matrices
The edges of a graph are represented using a matrix. This representation works both with directed and undirected graphs. The n x n square matrix is denoted by A. n is the number of vertices in the graph. The semantics is Aij=1 if and only if there's an edge between vertices i and j in the graph. It can be extended for parallel arcs and weighted graphs. For parallel arcs, Aij denotes the number of edges. For weighted graphs, Aij denotes the weight of the edge. For directed graphs, if the arc is directed from i to j, Aij=+1 and if it is directed from j to i, Aij=-1.
An adjacency matrix requires space quadratic in the number of vertices Θ(n2). For dense graphs this is fine but for sparse graphs, it is wasteful.
Adjacency matrix representation is preferred for dense graphs or when we need to tell quickly if there is an edge connecting two given vertices.
More details in CLRS page 590.