Dijkstra's Shortest-Path Algorithm

External

• https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/rxrPa/dijkstras-shortest-path-algorithm
• https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/iIzo8/heaps-operations-and-applications
• https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/Jfvmn/dijkstras-algorithm-examples

Internal

• Shortest Path in a Graph

Overview

The problem of computing the shortest path in a graph can be solved with bread-first search, but the breadth-first search-based shortest path algorithm works in the special case when the length of every edge in the graph ℓe is 1. Dijkstra's shortest-path algorithm solves a more general problem, where the edges have arbitrary non-negative lengths.

The problem of computing the shortest path in a graph with arbitrary edge lengths can be theoretically reduced to the problem of computing the shortest path in a graph with edges of length ℓe=1, by replacing an edge with an arbitrary length n with n edges with length 1, and adding extra vertices. The breadth-first search-based shortest path algorithm would theoretically work fine in this situation, producing the same results as the Dijkstra's algorithm, but the problem is that we are increasing the size of the graph, in terms of adding extra nodes and edges, and this increase my be non-trivial: for an edge with length 1000, we need to add extra 999 edges and 999 extra nodes. This representation would be wasteful, and even if the breadth-first search-based shortest path algorithm works in linear time, it is on a much larger graph, and we would much prefer an linear-time (or close to linear-time algorithm) that achieves the same result on the smaller graph. This is exactly what the Dijkstra's algorithm accomplishes.

If all edges are unit-length edges, Dijkstra's becomes the breadth-first search-based algorithm.

The Problem

The single-source shortest paths is formally defined as follows: given a directed graph G=(V, E) , with n = │V│ and m=│E│, where each edge e has a non-negative length ℓ_e, and a source vertex s, compute for each v ∈ V the length L(v) of the shortest path s → v.

The assumption that the length is non-negative is important. Dijkstra's shortest-path algorithm does not work correctly in presence of negative length edges.

The Straightforward (Non-Optimized) Implementation

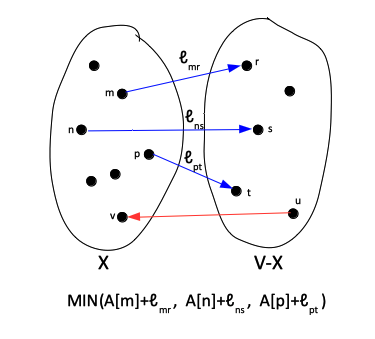
The general idea is to start at the source vertex s, and iterate in such a way that in each iteration we explore a new vertex and add it to the "explored territory". The new vertex is chosen in such a way that it minimizes Dijkstra's Greedy Criterion, as described below.

 Initialize X={s} # X is the set of vertices for which the shortest path to s has been computed so far
 Initialize A[s]={0} # A maintains computed shortest path distances from the vertices explored so far to s
 Initialize B[s]={empty path} # B maintains the actual shortest path distances from the vertices explored 
                              # so far to s. This is not necessary in the algorithm but helps with the 
                              # understanding of the algorithm.

 while X ≠ V: # The main loop, each iteration grows X with one node
     for every directed edge (v, w) ∈ E that crosses X/(V-X) boundary v ∈ V, w ∈ V-X
         pick edge that minimizes A[v] + ℓvw # The Dijkstra's Greedy Criterion
         # Call the edge (v*, w*)
     add w* to X
     set A[w*] = A[v*] + ℓv*w*
     set B[w*] = B[v*] ⋃ (v*,w*)

Examples

https://www.coursera.org/learn/algorithms-graphs-data-structures/lecture/Jfvmn/dijkstras-algorithm-examples

The Optimized Implementation

The Dijkstra's algorithm can be sped up with the use of a heap.