Fibonacci Numbers: Difference between revisions
Jump to navigation
Jump to search
| (7 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
* [[Mathematics]] | * [[Mathematics]] | ||
* [[Algorithms#Dynamic_Programming_Algorithms|Algorithms]] | |||
* [[Dynamic_Programming#Canonical_Use|Dynamic Programming]] | |||
=Overview= | =Overview= | ||
| Line 13: | Line 15: | ||
F<sub>i</sub> = F<sub>i-1</sub> + F<sub>i-2</sub> for i ≥ 2. | F<sub>i</sub> = F<sub>i-1</sub> + F<sub>i-2</sub> for i ≥ 2. | ||
<font color= | <font color=darkkhaki>TODO [[CLRS]] page 108.</font> | ||
=Golden Ratio= | =Golden Ratio= | ||
| Line 38: | Line 40: | ||
[[File:Fibonacci_Recursion_Tree.png|900px]] | [[File:Fibonacci_Recursion_Tree.png|900px]] | ||
This is a bad exponential time, and attempting to use the algorithm for anything larger than 50 gets problematic. The | Running time < 2<sup>0</sup> + 2<sup>1</sup> + ... + 2<sup>n-1</sup>. | ||
This is a bad exponential time, and attempting to use the algorithm for anything larger than 50 gets problematic. The fact that we're redundantly computing the same values again and again provides a hint that we could use a [[#Dynamic_Programming|dynamic programming]] method: | |||
==Dynamic Programming== | ==Dynamic Programming== | ||
<syntaxhighlight lang='java'> | |||
public static long fib_dp(int n) { | |||
long[] a = new long[n + 1]; | |||
a[0] = 0; | |||
a[1] = 1; | |||
for(int i = 2; i <= n; i ++) { | |||
a[i] = a[i-1] + a[i-2]; | |||
} | |||
return a[n]; | |||
} | |||
</syntaxhighlight> | |||
Also see: {{Algorithms#Dynamic_Programming_Algorithms|Dynamic Programming Algorithms}} | |||
Latest revision as of 21:53, 11 November 2021
Internal
Overview
We define Fibonacci numbers by the following recurrence:
F0 = 0
F1 = 1
Fi = Fi-1 + Fi-2 for i ≥ 2.
TODO CLRS page 108.
Golden Ratio
φ=1.6180339...
Algorithms
Straightforward Recursive
A straightforward recursive algorithm looks like this:
public static long fib(long n) {
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
return fib(n - 1) + fib(n - 2);
}
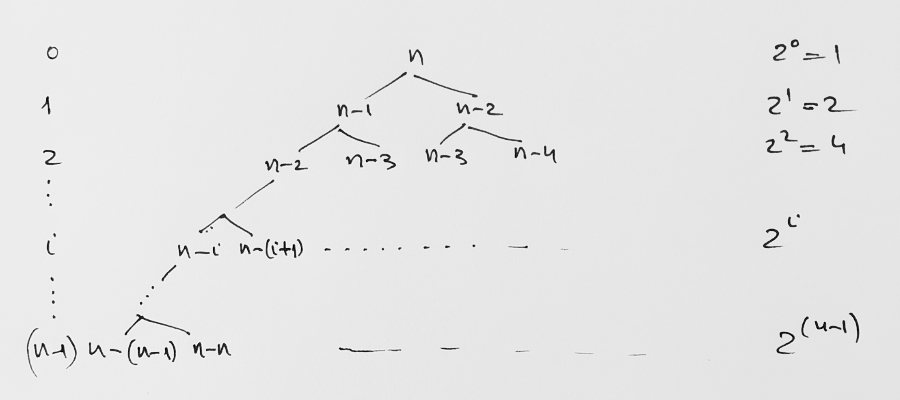
However, the running time of this method, computed with a recursion tree, is O(2n):
Running time < 20 + 21 + ... + 2n-1.
This is a bad exponential time, and attempting to use the algorithm for anything larger than 50 gets problematic. The fact that we're redundantly computing the same values again and again provides a hint that we could use a dynamic programming method:
Dynamic Programming
public static long fib_dp(int n) {
long[] a = new long[n + 1];
a[0] = 0;
a[1] = 1;
for(int i = 2; i <= n; i ++) {
a[i] = a[i-1] + a[i-2];
}
return a[n];
}
Also see: Template:Algorithms