Fibonacci Numbers: Difference between revisions
Jump to navigation
Jump to search
| (2 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
* [[Mathematics]] | * [[Mathematics]] | ||
* [[Algorithms#Dynamic_Programming_Algorithms|Algorithms]] | * [[Algorithms#Dynamic_Programming_Algorithms|Algorithms]] | ||
* [[Dynamic_Programming#Canonical_Use|Dynamic Programming]] | |||
=Overview= | =Overview= | ||
| Line 55: | Line 56: | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Also see: {{Algorithms#Dynamic_Programming_Algorithms|Dynamic Programming Algorithms}} | |||
Latest revision as of 21:53, 11 November 2021
Internal
Overview
We define Fibonacci numbers by the following recurrence:
F0 = 0
F1 = 1
Fi = Fi-1 + Fi-2 for i ≥ 2.
TODO CLRS page 108.
Golden Ratio
φ=1.6180339...
Algorithms
Straightforward Recursive
A straightforward recursive algorithm looks like this:
public static long fib(long n) {
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
return fib(n - 1) + fib(n - 2);
}
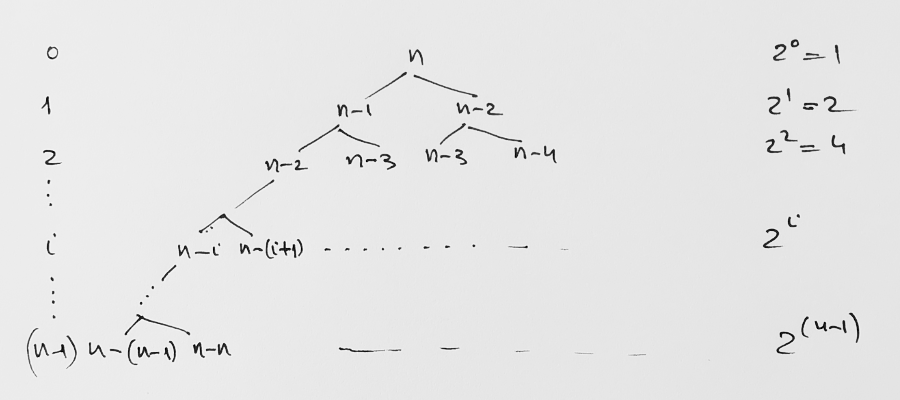
However, the running time of this method, computed with a recursion tree, is O(2n):
Running time < 20 + 21 + ... + 2n-1.
This is a bad exponential time, and attempting to use the algorithm for anything larger than 50 gets problematic. The fact that we're redundantly computing the same values again and again provides a hint that we could use a dynamic programming method:
Dynamic Programming
public static long fib_dp(int n) {
long[] a = new long[n + 1];
a[0] = 0;
a[1] = 1;
for(int i = 2; i <= n; i ++) {
a[i] = a[i-1] + a[i-2];
}
return a[n];
}
Also see: Template:Algorithms