Tree Concepts: Difference between revisions
(→Root) |
|||
| (100 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
# Any two vertices in G are connected by a unique [[Graph_Concepts#Simple_Path|simple path]]. | # Any two vertices in G are connected by a unique [[Graph_Concepts#Simple_Path|simple path]]. | ||
# G is [[Graph_Concepts#Connectivity_and_Graph_Components|connected]], but if any edge is removed from E, the resulting graph is disconnected. | # G is [[Graph_Concepts#Connectivity_and_Graph_Components|connected]], but if any edge is removed from E, the resulting graph is disconnected. | ||
# G is connected and | # G is connected and │E│ = │V│ - 1. | ||
# G is acyclic and | # G is acyclic and │E│ = │V│ - 1. | ||
# G is acyclic, but if any edge is added to E, the resulting graph contains a cycle. | # G is acyclic, but if any edge is added to E, the resulting graph contains a cycle. | ||
=Forest= | |||
If the undirected graph is acyclic, but [[Graph_Concepts#Connectivity_and_Graph_Components|disconnected]], it is a [[Graph_Concepts#Forest|forest]]. | If the undirected graph is acyclic, but [[Graph_Concepts#Connectivity_and_Graph_Components|disconnected]], it is a [[Graph_Concepts#Forest|forest]]. | ||
:::[[Image:Graph_Forest.png]] | :::[[Image:Graph_Forest.png]] | ||
=Search Tree= | =Rooted Tree= | ||
A '''rooted tree''' is a [[#Free_Tree|free tree]] in which one of the vertices is distinguished from the others. | |||
:::[[File:Tree_Height_and_Depth.png|551px]] | |||
==Root== | |||
We call the distinguished vertex the '''root''' of the tree. A room has no parent. | |||
A root is at the same time a [[#Leaf|leaf]] in case of a single node tree. In this case, the single node would fulfill both the role of a root, as it has no parent, and that of a leaf, as it has children. | |||
==Node== | |||
We often refer to the [[Graph_Concepts#Vertex|vertex]] of a rooted tree as a '''node''' of the tree. | |||
==<span id='Ancestor'></span><span id='Descendant'></span>Ancestors and Descendants== | |||
For a node x in a rooted tree, we call any node y on the simple path from root to x an '''ancestor''' of x. If y is an ancestor of x, then x is a '''descendant''' of y. Every node is both an ancestor and descendant of itself. If y is an ancestor of x and x ≠ y, then we call y a '''proper ancestor''' of x, and x is a '''proper descendant''' of y. | |||
==Subtree== | |||
The '''subtree rooted at x''' is the tree induced by descendants of x, rooted at x. | |||
==<span id='Parent'></span><span id='Child'></span><span id='Children'></span>Parents, Children and Siblings== | |||
If the last edge on the simple path from the root of the tree to a node x is (y, x), then y is the '''parent''' of x and x is the '''child''' of y. The root is the only node in the tree with no parent. If two nodes have the same parent, they are '''siblings'''. | |||
==Leaf== | |||
A node with no children is a '''leaf''' or an '''external node'''. A non-leaf node is an '''internal node'''. | |||
==Depth and Height== | |||
===Depth=== | |||
The [[Graph_Concepts#Path_Length|length]] of the simple path from the [[#Root|root]] to a node x, measured in the number of edges, is called the '''depth''' of the node x in the tree. The depth is always relative to the root. | |||
===Level=== | |||
A '''level''' of a tree consists of all nodes at the same [[#Depth|depth]]. | |||
===Height=== | |||
The '''height of a node''' in a tree is the number of edges on the '''longest''' simple downward path from the node in question to a leaf. | |||
The '''height of the tree''' is the height of its root. The height of the tree is also equal to the largest depth of any node in the tree. | |||
The height is always relative to the lowest leaf. | |||
=Degree= | |||
Note that the '''degree''' of a node depends on whether we consider the tree to be a [[#Rooted_Tree|rooted tree]] or a [[#Free_Tree|free tree]]. | |||
In case of a free tree, the degree of a node is the degree of a vertex in an [[Graph_Concepts#Undirected_Graph|undirected graph]], defined as [[Graph_Concepts#Vertex_Degree|the number of adjacent vertices]]. | |||
For a rooted tree, the degree is the number of [[#Children|children]]. The parent of the node does not count toward its degree. | |||
=Ordered Tree= | |||
An '''ordered tree''' is a [[#Rooted_Tree|rooted tree]] in which the children of each node are ordered. If a node has k children, then there is a first child, a second child, and the k<sup>th</sup> child. Also see [[#Ordered_and_Binary_Trees|Difference between Binary Trees and Ordered Trees]]. | |||
=Positional Tree= | |||
In a '''positional tree''', the children of a node are labeled with distinct positive integers. The i<sup>th</sup> child of a node is '''absent''' if no child is labeled with integer i. | |||
=<span id=K-ary'></span>K-ary Tree= | |||
A '''k-ary''' tree is a [[#Positional_Tree|positional tree]] in which for every node, all children with labels greater than k are absent. | |||
A <span id='Complete_K-ary_Tree'></span>'''complete k-ary tree''' is a k-ary tree in which all leaves have the same depth and all internal nodes have degree k. | |||
==K-ary Tree Arithmetic== | |||
:::[[Image:Tree_K-ary.png]] | |||
A complete k-ary tree of height h has k<sup>0</sup> + k<sup>1+</sup> + ... + k<sup>h-1</sup> = (k<sup>h</sup> - 1)/(k - 1) nodes and k<sup>h</sup> leaves. | |||
The height of a complete k-ary tree with n leaves is log<sub>k</sub>n. | |||
==Types of K-ary Trees== | |||
===B and B+ Trees=== | |||
{{Internal|B and B+ Trees|B and B+ Trees}} | |||
=<span id='Sorting_Tree'></span>Search Tree= | |||
* [[Binary_Search_Trees#Overview|Binary search tree]] | |||
* [[B_and_B%2B_Trees|B tree]] | |||
=Binary Tree= | =Binary Tree= | ||
A '''binary tree''' is defined recursively as a structure defined on a finite set of nodes that either: | |||
* contains no nodes | |||
* is composed of three disjoint sets of nodes: a '''root''' node, a binary tree called its '''left subtree''' and a binary tree called its '''right subtree'''. | |||
If the left subtree is not empty, its root is called the '''left child''' of the root of the entire tree. If the right subtree is not empty, its root is called the '''right child''' of the root of the entire tree. | |||
A binary tree can also be defined as a [[#K-ary|k-ary]] tree with k=2. | |||
==Types of Binary Trees== | |||
====Full Binary Tree==== | |||
A '''full''' binary tree, sometimes referred to as a '''proper''' or '''plane''' binary tree, is a tree in which every node has either 0 or 2 children. Each node is either a [[#Leaf|leaf]] or has a [[#Degree|degree]] of exactly 2, and there are no degree-1 nodes. No node can have just one child. A full binary tree can also be defined with the recursive definition: a full binary tree is either a single node or a tree whose node has two subtrees, both of which are fully binary trees. | |||
:::::::[[File:Full_Tree.png|272px]] | |||
====<span id='As_Complete_as_Possible'></span>Complete Binary Tree==== | |||
A '''complete''' binary tree is a tree in which every level, except possibly the last, is completely filled and all nodes in the last level are as far left as possible. These tree are sometimes referred to as '''almost complete''', '''nearly complete''', or '''as complete as possible'''. A complete binary tree can be efficiently represented using an array, so this property of binary trees is relevant when building [[Heap#Overview|heaps]]. | |||
:::[[File:Complete_Tree.png|488px]] | |||
====Perfect Binary Tree==== | |||
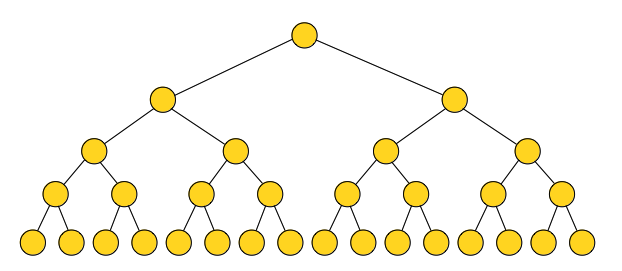
A '''perfect''' binary tree is a tree that is both [[#Full_Binary_Tree|full]] and [[#Complete_Binary_Tree|complete]]. All leaf nodes will be at the same level, and this level will have the maximum number of nodes. | |||
:::[[File:Perfect_Tree.png|622px]] | |||
The size of a perfect binary tree as a function of its depth d is 2<sup>d</sup>-1 nodes. | |||
====Balanced Binary Tree==== | |||
Usually, "as balanced as possible" means balanced enough to ensure O(n log n) for [[Data_Structures#INSERT.28X.29|INSERT]] and [[Data_Structures#SEARCH.28K.29|SEARCH]]. | |||
==<span id='Ordered_and_Binary_Trees'></span>Difference between Binary Trees and Ordered Trees== | |||
A binary tree isn't simply an [[#Ordered_Tree|ordered]] tree with a [[#Degree|degree]] of at most 2. In an ordered tree, there is no distinguishing a sole child as being either left or right. For a binary tree, the left or right position matters, so from this perspective, the concept of binary tree is stronger than the one of ordered tree. Binary trees can be implemented using ordered trees, if we maintain the position information necessary to a binary tree by replacing each missing child in the binary tree with a node having no children. | |||
==<span id='Balanced_Binary_Search_Tree'></span><span id='Red-Black_Trees'></span><span id='AVL_Trees'></span><span id='Splay_Trees'></span>Binary Search Tree== | |||
These include [[Binary_Search_Trees#Balanced_Binary_Search_Trees|balanced binary search trees]], [[Red-black_Tree#Overview|red-black trees]], [[AVL_Trees#Overview|AVL trees]], [[Splay_Trees#Overview|splay trees]]: | |||
{{Internal|Binary_Search_Trees#Overview|Binary Search Trees}} | |||
=<span id='Trie'></span><span id='Radix_Tree'></span>Radix Trees (Tries)= | |||
{{Internal|Tries|Tries}} | |||
=Heaps= | |||
{{Internal|Heap#Overview|Heaps}} | |||
=Burst Trees= | |||
<font color=darkkhaki>TODO: Learning/CS Fundamentals/Algorithms/Burst Tries.pdf</font> | |||
== | =Tree Traversal= | ||
{{Internal|Tree Traversal|Tree Traversal}} | |||
=Degenerated (Pathological) Tree= | |||
A degenerate (or pathological) tree is where each parent node has only one associated child node. This means that the tree will behave like a linked list data structure. | |||
Latest revision as of 00:48, 3 November 2024
Internal
Overview
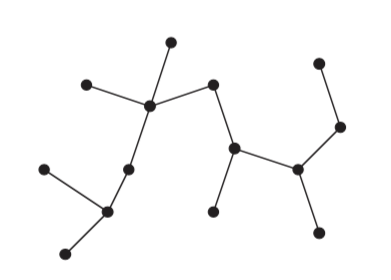
A tree is a particular case of a graph.
Free Tree
A free tree is a connected, acyclic, undirected graph.
For an undirected graph G = (V, E), the following statements are equivalent:
- G is a free tree.
- Any two vertices in G are connected by a unique simple path.
- G is connected, but if any edge is removed from E, the resulting graph is disconnected.
- G is connected and │E│ = │V│ - 1.
- G is acyclic and │E│ = │V│ - 1.
- G is acyclic, but if any edge is added to E, the resulting graph contains a cycle.
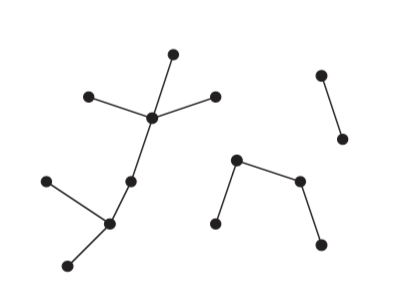
Forest
If the undirected graph is acyclic, but disconnected, it is a forest.
Rooted Tree
A rooted tree is a free tree in which one of the vertices is distinguished from the others.
Root
We call the distinguished vertex the root of the tree. A room has no parent.
A root is at the same time a leaf in case of a single node tree. In this case, the single node would fulfill both the role of a root, as it has no parent, and that of a leaf, as it has children.
Node
We often refer to the vertex of a rooted tree as a node of the tree.
Ancestors and Descendants
For a node x in a rooted tree, we call any node y on the simple path from root to x an ancestor of x. If y is an ancestor of x, then x is a descendant of y. Every node is both an ancestor and descendant of itself. If y is an ancestor of x and x ≠ y, then we call y a proper ancestor of x, and x is a proper descendant of y.
Subtree
The subtree rooted at x is the tree induced by descendants of x, rooted at x.
Parents, Children and Siblings
If the last edge on the simple path from the root of the tree to a node x is (y, x), then y is the parent of x and x is the child of y. The root is the only node in the tree with no parent. If two nodes have the same parent, they are siblings.
Leaf
A node with no children is a leaf or an external node. A non-leaf node is an internal node.
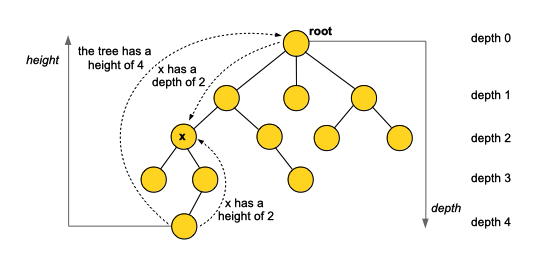
Depth and Height
Depth
The length of the simple path from the root to a node x, measured in the number of edges, is called the depth of the node x in the tree. The depth is always relative to the root.
Level
A level of a tree consists of all nodes at the same depth.
Height
The height of a node in a tree is the number of edges on the longest simple downward path from the node in question to a leaf.
The height of the tree is the height of its root. The height of the tree is also equal to the largest depth of any node in the tree.
The height is always relative to the lowest leaf.
Degree
Note that the degree of a node depends on whether we consider the tree to be a rooted tree or a free tree.
In case of a free tree, the degree of a node is the degree of a vertex in an undirected graph, defined as the number of adjacent vertices.
For a rooted tree, the degree is the number of children. The parent of the node does not count toward its degree.
Ordered Tree
An ordered tree is a rooted tree in which the children of each node are ordered. If a node has k children, then there is a first child, a second child, and the kth child. Also see Difference between Binary Trees and Ordered Trees.
Positional Tree
In a positional tree, the children of a node are labeled with distinct positive integers. The ith child of a node is absent if no child is labeled with integer i.
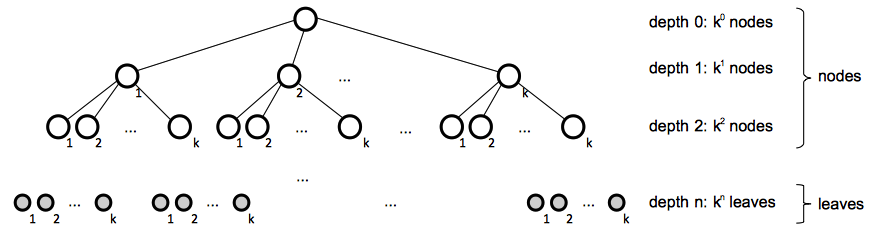
K-ary Tree
A k-ary tree is a positional tree in which for every node, all children with labels greater than k are absent.
A complete k-ary tree is a k-ary tree in which all leaves have the same depth and all internal nodes have degree k.
K-ary Tree Arithmetic
A complete k-ary tree of height h has k0 + k1+ + ... + kh-1 = (kh - 1)/(k - 1) nodes and kh leaves.
The height of a complete k-ary tree with n leaves is logkn.
Types of K-ary Trees
B and B+ Trees
Search Tree
Binary Tree
A binary tree is defined recursively as a structure defined on a finite set of nodes that either:
- contains no nodes
- is composed of three disjoint sets of nodes: a root node, a binary tree called its left subtree and a binary tree called its right subtree.
If the left subtree is not empty, its root is called the left child of the root of the entire tree. If the right subtree is not empty, its root is called the right child of the root of the entire tree.
A binary tree can also be defined as a k-ary tree with k=2.
Types of Binary Trees
Full Binary Tree
A full binary tree, sometimes referred to as a proper or plane binary tree, is a tree in which every node has either 0 or 2 children. Each node is either a leaf or has a degree of exactly 2, and there are no degree-1 nodes. No node can have just one child. A full binary tree can also be defined with the recursive definition: a full binary tree is either a single node or a tree whose node has two subtrees, both of which are fully binary trees.
Complete Binary Tree
A complete binary tree is a tree in which every level, except possibly the last, is completely filled and all nodes in the last level are as far left as possible. These tree are sometimes referred to as almost complete, nearly complete, or as complete as possible. A complete binary tree can be efficiently represented using an array, so this property of binary trees is relevant when building heaps.
Perfect Binary Tree
A perfect binary tree is a tree that is both full and complete. All leaf nodes will be at the same level, and this level will have the maximum number of nodes.
The size of a perfect binary tree as a function of its depth d is 2d-1 nodes.
Balanced Binary Tree
Usually, "as balanced as possible" means balanced enough to ensure O(n log n) for INSERT and SEARCH.
Difference between Binary Trees and Ordered Trees
A binary tree isn't simply an ordered tree with a degree of at most 2. In an ordered tree, there is no distinguishing a sole child as being either left or right. For a binary tree, the left or right position matters, so from this perspective, the concept of binary tree is stronger than the one of ordered tree. Binary trees can be implemented using ordered trees, if we maintain the position information necessary to a binary tree by replacing each missing child in the binary tree with a node having no children.
Binary Search Tree
These include balanced binary search trees, red-black trees, AVL trees, splay trees:
Radix Trees (Tries)
Heaps
Burst Trees
TODO: Learning/CS Fundamentals/Algorithms/Burst Tries.pdf
Tree Traversal
Degenerated (Pathological) Tree
A degenerate (or pathological) tree is where each parent node has only one associated child node. This means that the tree will behave like a linked list data structure.