Tree Concepts: Difference between revisions
| Line 32: | Line 32: | ||
====<span id='Ancestor'></span><span id='Descendant'></span>Ancestors and Descendants==== | ====<span id='Ancestor'></span><span id='Descendant'></span>Ancestors and Descendants==== | ||
For a node x in a rooted tree, we call any node y on the simple path from root to x an '''ancestor''' of x. If y is an ancestor of x, then x is a '''descendant''' of y. Every node is both an ancestor and descendant of itself. If y is an ancestor of x and x ≠ y, then we call y a '''proper ancestor''' of x, and x is a '''proper descendant''' of y. | For a node x in a rooted tree, we call any node y on the simple path from root to x an '''ancestor''' of x. If y is an ancestor of x, then x is a '''descendant''' of y. Every node is both an ancestor and descendant of itself. If y is an ancestor of x and x ≠ y, then we call y a '''proper ancestor''' of x, and x is a '''proper descendant''' of y. | ||
====Subtree==== | |||
The '''subtree rooted at x''' is the tree induced by descendants of x, rooted at x. | The '''subtree rooted at x''' is the tree induced by descendants of x, rooted at x. | ||
====<span id='Parent'></span><span id='Child'></span>Parents, Children and Siblings==== | |||
<span id='Parent'></span><span id='Child'></span>If the last edge on the simple path from the root of the tree to a node x is (y, x), then y is the '''parent''' of x and x is the '''child''' of y. The root is the only node in the tree with no parent. | If the last edge on the simple path from the root of the tree to a node x is (y, x), then y is the '''parent''' of x and x is the '''child''' of y. The root is the only node in the tree with no parent. If two nodes have the same parent, they are '''siblings'''. | ||
If two nodes have the same parent, they are '''siblings'''. | |||
<span id='Leaf'></span>A node with no children is a '''leaf''' or an '''external node'''. A non-leaf node is an '''internal node'''. | <span id='Leaf'></span>A node with no children is a '''leaf''' or an '''external node'''. A non-leaf node is an '''internal node'''. | ||
Revision as of 20:42, 9 October 2021
Internal
Overview
A tree is a particular case of a graph.
Free Tree
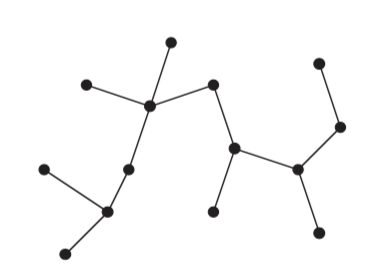
A free tree is a connected, acyclic, undirected graph.
For an undirected graph G = (V, E), the following statements are equivalent:
- G is a free tree.
- Any two vertices in G are connected by a unique simple path.
- G is connected, but if any edge is removed from E, the resulting graph is disconnected.
- G is connected and │E│ = │V│ - 1.
- G is acyclic and │E│ = │V│ - 1.
- G is acyclic, but if any edge is added to E, the resulting graph contains a cycle.
Forest
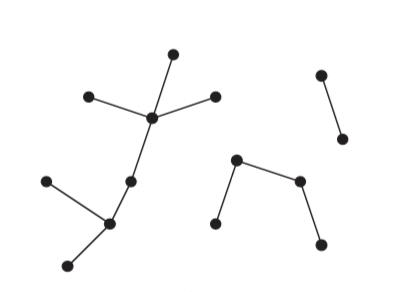
If the undirected graph is acyclic, but disconnected, it is a forest.
Rooted Tree
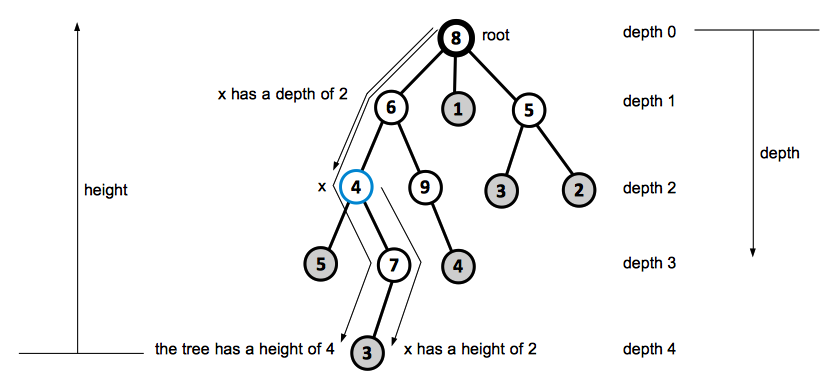
A rooted tree is a free tree in which one of the vertices is distinguished from the others.
Root
We call the distinguished vertex the root of the tree.
Node
We often refer to the vertex of a rooted tree as a node of the tree.
Ancestors and Descendants
For a node x in a rooted tree, we call any node y on the simple path from root to x an ancestor of x. If y is an ancestor of x, then x is a descendant of y. Every node is both an ancestor and descendant of itself. If y is an ancestor of x and x ≠ y, then we call y a proper ancestor of x, and x is a proper descendant of y.
Subtree
The subtree rooted at x is the tree induced by descendants of x, rooted at x.
Parents, Children and Siblings
If the last edge on the simple path from the root of the tree to a node x is (y, x), then y is the parent of x and x is the child of y. The root is the only node in the tree with no parent. If two nodes have the same parent, they are siblings.
A node with no children is a leaf or an external node. A non-leaf node is an internal node.