Fibonacci Numbers

Internal

• Mathematics

Overview

We define Fibonacci numbers by the following recurrence:

F₀ = 0

F₁ = 1

F_i = F_i-1 + F_i-2 for i ≥ 2.

TODO CLRS page 108.

Golden Ratio

φ=1.6180339...

Algorithms

Straightforward Recursive

A straightforward recursive algorithm looks like this:

public static long fib(long n) {
  if (n == 0) {
    return 0;
  }
  if (n == 1) {
    return 1;
  }
  return fib(n - 1) + fib(n - 2);
}

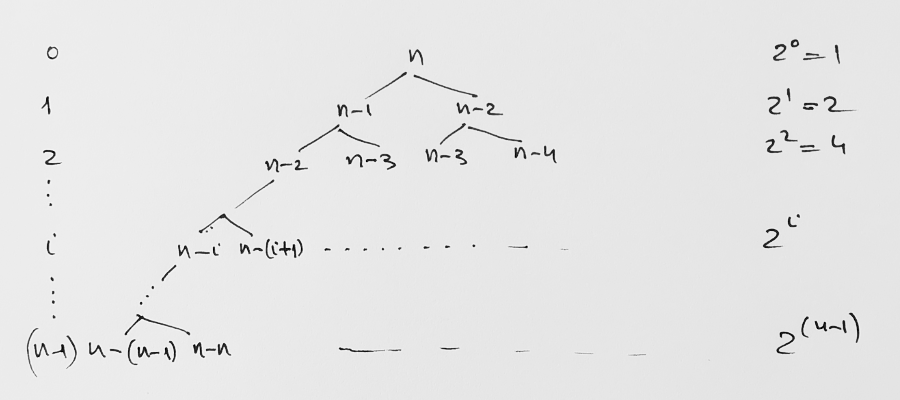
However, the running time of this method, computed with a recursion tree, is O(2ⁿ):

Running time < 2⁰ + 2¹ + ... + 2^n-1.

This is a bad exponential time, and attempting to use the algorithm for anything larger than 50 gets problematic. The solution is to apply a dynamic programming method:

Dynamic Programming

public static long fib_dp(int n) {
  long[] a = new long[n + 1];
  a[0] = 0;
  a[1] = 1;
  for(int i = 2; i <= n; i ++) {
    a[i] = a[i-1] + a[i-2];
  }
  return a[n];
}