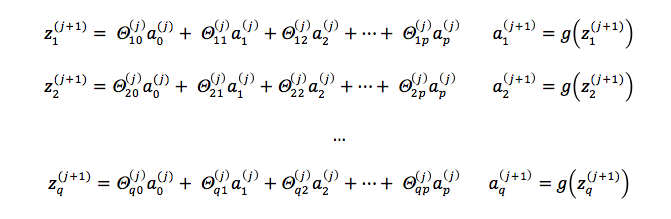Neural Networks

Internal

• Machine Learning

Individual Neuron

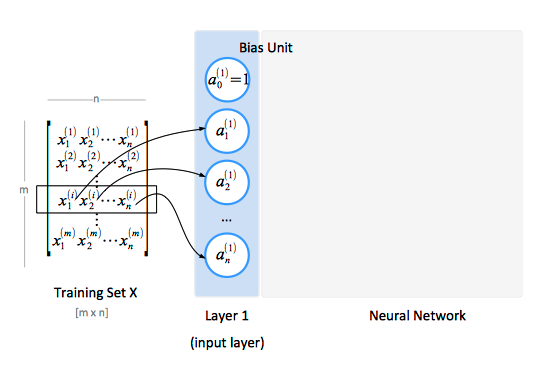
Individual neurons are computational units that read input features, represented as an unidimensional vector x1 ... xn in the diagram below, and calculate the hypothesis function as output. Note that x0 is not part of the feature vector, but it represents a bias value for the unit. The output value of the hypothesis function is also called the "activation" of the unit.

A common option is to use a logistic function as hypothesis, thus the unit is referred to as a logistic unit with a sigmoid (logistic) activation function.

The θ vector represents the model's parameters (model's weights). For a multi-layer neural network, the model parameters are collected in matrices named Θ, which will be describe below.

The x0 input node is called the bias unit, and it is optional. When provided, it is equal with 1.

Multi-Layer Neural Network

Notations

a_i^(j) represents the "activation" of unit i in layer j.

The Input Layer

The input nodes are known as the input layer, which is also conventionally named "layer 1". The input layer gets fed the training values. A training set contains a number of samples (m), and each sample has a number of features (n). The features of the training set are conventionally represented as a matrix X.

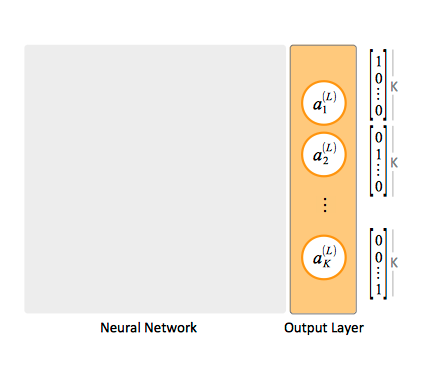
The Output Layer

The Hidden Layers

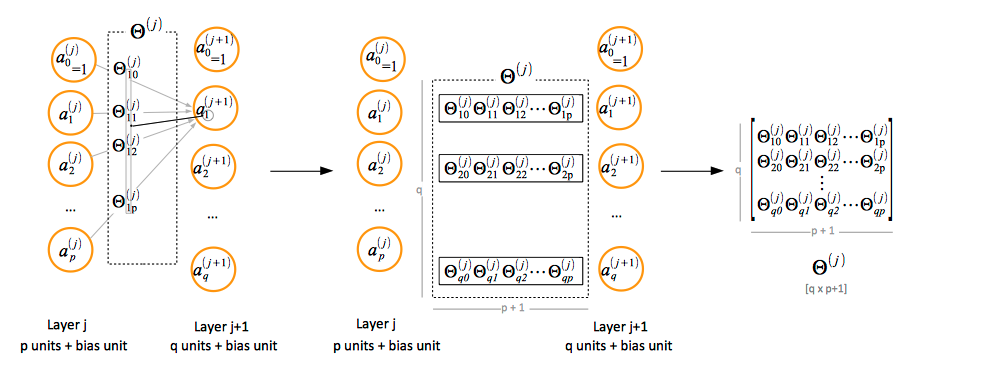
Paramenter Matrix Θ Notation Convention

If the layer j has p units, not counting the bias unit, and layer j + 1 has q units, not counting the bias unit, then the parameter matrix Θ(j) that determines the activation values for layer j + 1 units has q x (p + 1) elements. The "+1" comes from the addition of the bias node in layer j.

Layer j + 1 Unit Activation Values