The Minimum Spanning Tree Problem: Difference between revisions
Jump to navigation
Jump to search
| Line 14: | Line 14: | ||
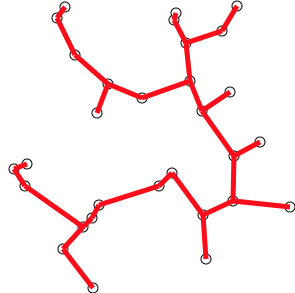
Given an [[Graph_Concepts#Undirected_Graph|undirected]] graph G=(V, E) and a positive or negative cost c<sub>e</sub> for each edge e ∈ E, find the minimum [[Graph_Concepts#Spanning_Tree_Cost|cost]] [[Graph_Concepts#Spanning_Trees|spanning tree]] T ⊆ E. | Given an [[Graph_Concepts#Undirected_Graph|undirected]] graph G=(V, E) and a positive or negative cost c<sub>e</sub> for each edge e ∈ E, find the minimum [[Graph_Concepts#Spanning_Tree_Cost|cost]] [[Graph_Concepts#Spanning_Trees|spanning tree]] T ⊆ E. | ||
:::[[File:MinimumCostSpanningTree.png]] | |||
=Algorithms= | =Algorithms= | ||
==Prim's Algorithm== | ==Prim's Algorithm== | ||
Revision as of 21:58, 20 October 2021
External
Internal
Overview
We discuss the minimum spanning problem in the context of undirected graphs. The same problem can be discussed for directed graphs but in that case it is referred to as the Optimal Branching Problem.
The Problem
Given an undirected graph G=(V, E) and a positive or negative cost ce for each edge e ∈ E, find the minimum cost spanning tree T ⊆ E.