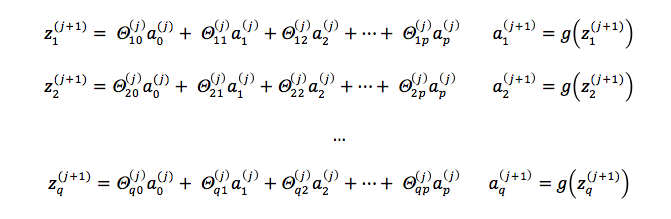Neural Networks

Internal

• Machine Learning

Individual Unit

Individual neural network units are computational units that read input features, represented as an unidimensional vector x₁ ... x_n in the diagram below, and calculate the hypothesis function as output of the unit. Note that x₀ is not part of the feature vector, but it represents a bias value for the unit. The output value of the hypothesis function is also called the "activation" of the unit.

A common option is to use a logistic function as hypothesis, thus the unit is referred to as a logistic unit with a sigmoid (logistic) activation function.

The θ vector represents the model's parameters (model's weights). For a multi-layer neural network, the model parameters are collected in matrices named Θ, which will be describe below.

The x0 input node is called the bias unit, and it is optional. When provided, it is equal with 1.

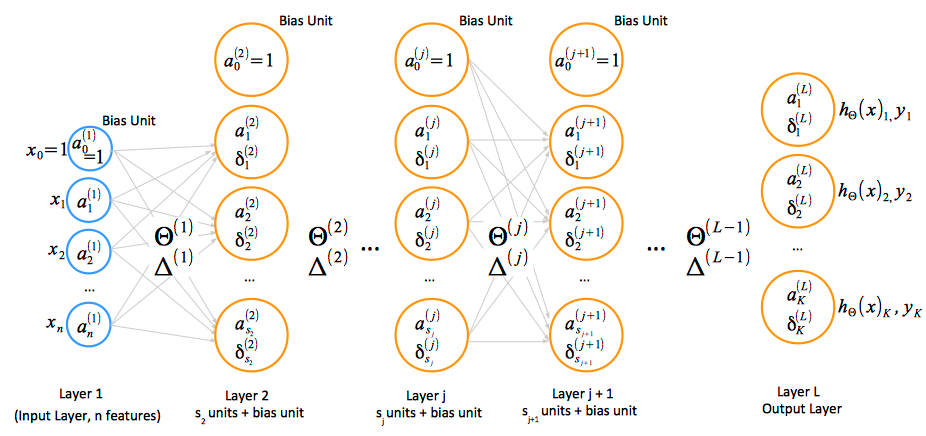
Multi-Layer Neural Network

Notations and Conventions

activation: a_i^(j) represents the "activation" of unit i in layer j. The input values x can be thought of as the activations of the input layer, conventionally named layer 1, and so they can be consistently named a₁⁽¹⁾, a₂⁽¹⁾, ... a_n⁽¹⁾. The input bias unit is a₀⁽¹⁾=1.

parameter matrix Θ: Θ^(j) represents the matrix of parameters (weights) that controls function mapping from layer j to layer j + 1.

forward propagation: A vectorized implementation of the forward propagation algorithm is available in the "Layer j + 1 Forward Propagation Vectorized Implementation" section.

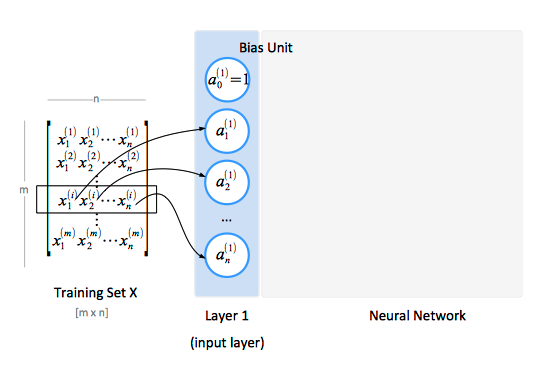
The Input Layer

The input layer, conventionally named "layer 1", consists of input nodes. The input layer provides the training values. A training set contains a number of samples (m), and each sample has a number of features (n). The features of the training set are conventionally represented as a matrix X.

The Hidden Layers

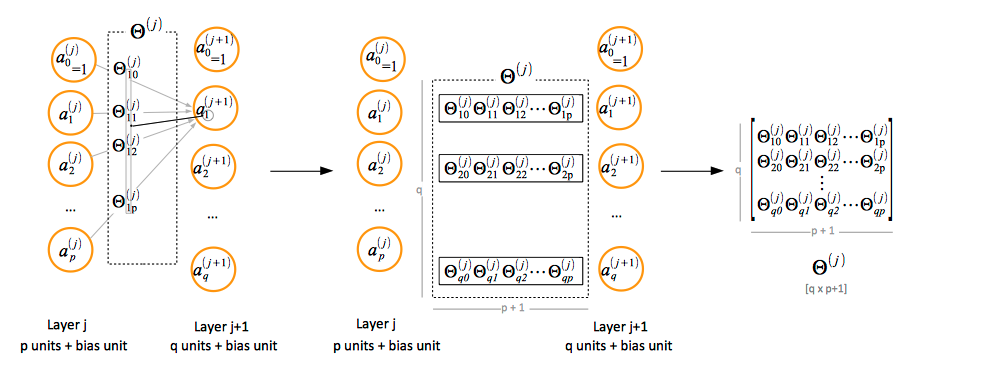
Paramenter Matrix Θ Notation Convention

If the layer j has p units, not counting the bias unit, and layer j + 1 has q units, not counting the bias unit, then the parameter matrix Θ^(j) controlling function mapping from layer j to layer j + 1 has q x (p + 1) elements. The "+1" comes from the addition of the bias node in layer j.

Layer j + 1 Unit Activation Values

In order to compute the activation values of a layer j + 1, we calculate the weighted linear combination of the input values (or the activation values of the previous layer), conventionally named z_i^{(j + 1)} and then we apply the logistic function to the result.

The Output Layer