Neural Networks
Internal
Overview
A neural network consists of several layers of activation units ("individual neurons"), where one layer's activation unit output is connected to the inputs of all activation units of the successive layer. The behavior of an individual activation unit is described in the "Individual Unit" section. A neural network's topology, along with conventions and notations - which are essential to get right if you want to follow the linear algebra equations - are discussed in the "Topology" section.
A neural network produces predictions by forward propagating input, then activations across its layers from left to right, until the output layer computes the hypothesis function, for a specific input sample.
A single activation unit has a function identical to, and works similarly with logistic regression, but instead of applying the logistic function only to a set of input features, it is applied successively to the input features and to activation values of intermediate layers. The intuition behind this behavior is that a neural network gets to learn its own internal features, often across several layers, instead of being constrained to process the input features and immediately produce a result. Practice shows that the network may learn interesting and complex features, which can lead to a better hypothesis.
The forward propagation process is described in detail in the "Forward Propagation" section.
Forward propagation computations are performed based on a set of parameters (or weights) that are obtained by training the network. Training the network, or "fitting the parameters", is performed by a backpropagation algorithm, which is described in the "Backpropagation" section.
Individual Unit
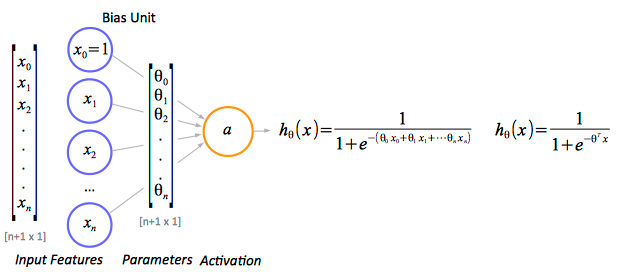
Individual neural network units are computational units that read input features, represented as an unidimensional vector x1 ... xn in the diagram below, and calculate the hypothesis function as output of the unit. The result of the hypothesis function is also called the "activation" of the unit.
Input Feature
In context of an individual processing unit, the input feature refers to an individual value fed to a single input of the unit. For units in the first layer, the features are individual elements of the input matrix, while for units in the hidden layers or the output layers, the features are the activation values of the computational units from the previous layer.
The input features are grouped into an input vector.
In most cases, an additional constant value x0=1 is added to the feature vector. x0 is not part of the feature vector, but it represents a bias value for the unit. In a multi-layer neural network, the bias values are provided by bias units.
Activation
The output value of the hypothesis function is also called the "activation" of the unit and it is conventionally named ai(j), where j is the layer the unit belongs to, and i is the index of the unit in the layer. For more details on notation, see Topology section below. The activation value is calculated by applying the logistic function to a linear combination of input features and parameters, thus the unit is referred to as a logistic unit with a sigmoid (logistic) activation function.
Parameters
Parameters are real values that are applied to the input vector as a linear combination. For neural networks, they are also known as weights. Conventionally, they are named θ (theta), and for a multi-layer neural network, the model parameters are collected in matrices named Θ. The naming convention is described in detail in the Topology section.