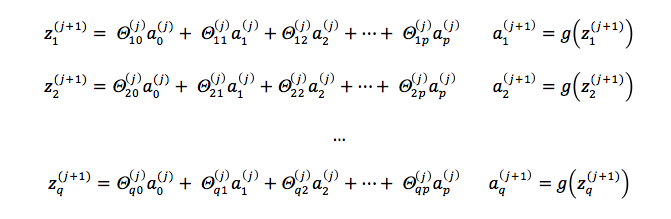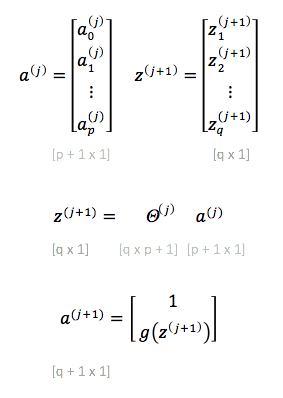Neural Networks

Internal

• Machine Learning

Overview

A neural network consists of several layers of activation units ("individual units" or "individual neurons"), where the output of one unit is connected to the inputs of all units of the successive layer. The behavior of an individual activation unit is described in the "Individual Unit" section. A neural network's topology, along with conventions and notations - which are essential to understand if you want to follow the linear algebra equations - are discussed in the "Topology" section.

A neural network produces predictions by forward propagating input, then activations, across its layers from left to right, until the output layer computes the hypothesis function, for a specific input sample. A single activation unit has a function similar to logistic regression, but instead of applying the logistic function only to a set of input features, it is applied successively to the input features and to activation values of intermediate layers. The intuition behind this behavior is that a neural network gets to learn its own internal features, often across several layers, instead of being constrained to process the input features and immediately produce a result. Practice shows that the network may learn interesting and complex features, which can lead to a better hypothesis.

The forward propagation process is described in detail in the "Forward Propagation" section.

Forward propagation computations are performed based on a set of parameters (or weights) that are obtained by training the network. Training the network, or "fitting the parameters", is performed by a backpropagation algorithm, which is described in the "Backpropagation" section.

Individual Unit

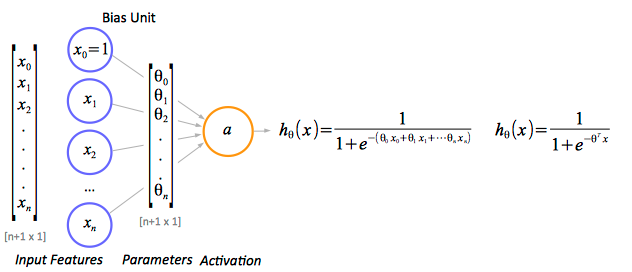
Individual neural network units are computational units that read input features, represented as an unidimensional vector x₁ ... x_n in the diagram below, and calculate the hypothesis function as output of the unit. The result of the hypothesis function is also called the "activation" of the unit.

Input Feature

In context of an individual processing unit, the input feature refers to an individual value fed to a single input of the unit. For units in the first layer, the features are individual elements of the input matrix, while for units in the hidden layers or the output layers, the features are the activation values of the computational units from the previous layer.

The input features are grouped into an input vector.

In most cases, an additional constant value x₀=1 is added to the feature vector. x₀ is not part of the feature vector, but it represents a bias value for the unit. In a multi-layer neural network, the bias values are provided by bias units.

Activation

The output value of the hypothesis function is also called the "activation" of the unit and it is conventionally named a_i^(j), where j is the layer the unit belongs to, and i is the index of the unit in the layer. For more details on notation, see Topology section below. The activation value is calculated by applying the logistic function to a linear combination of input features and parameters, thus the unit is referred to as a logistic unit with a sigmoid (logistic) activation function.

Parameters

Parameters are real values that are applied to the input vector as a linear combination. For neural networks, they are also known as weights. Conventionally, they are named θ (theta), and for a multi-layer neural network, the model parameters are collected in matrices named Θ. The naming convention is described in detail in the Topology section.

Topology

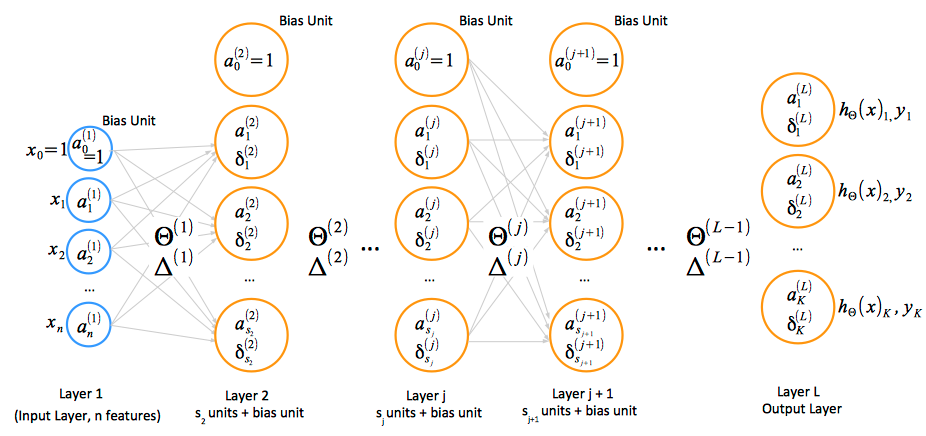
The total number of layers in the network is conventionally named L. Layer 1 is the input layer, layers 2, 3, ... L - 1 are the hidden layers, and layer L is the output layer.

The number of units in the layer l is conventionally named s_l. This number does not include the bias unit, so the total number of units in a layer, including the bias unit, is s_l + 1.

The total number of classes the network classifies, which is equal to the number of output units, is conventionally named K.

Activation a_i^(j) represents the activation of unit i in layer j. The input values x can be thought of as the activations of the input layer, conventionally named layer 1, and so they can be consistently named a₁⁽¹⁾, a₂⁽¹⁾, ... a_n⁽¹⁾. The input bias unit is a₀⁽¹⁾=1.

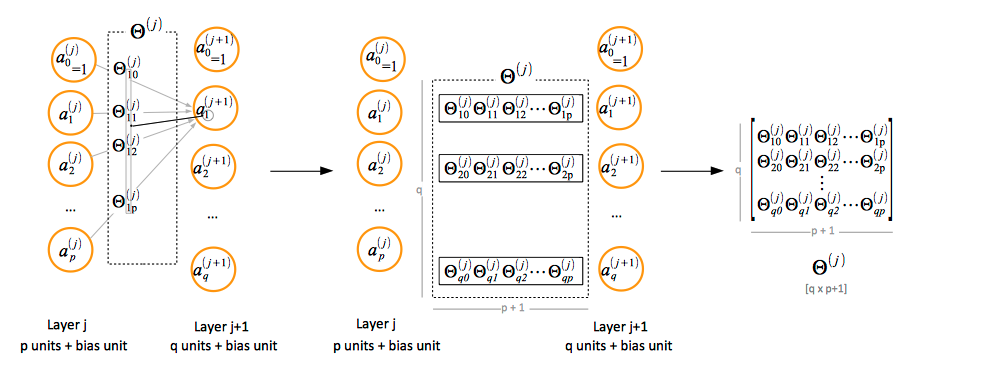
Θ^(j) represents the matrix of parameters (weights) that controls function mapping from layer j to layer j + 1. Details on how these parameters are used in computing activation values are available in the Forward Propagation section.

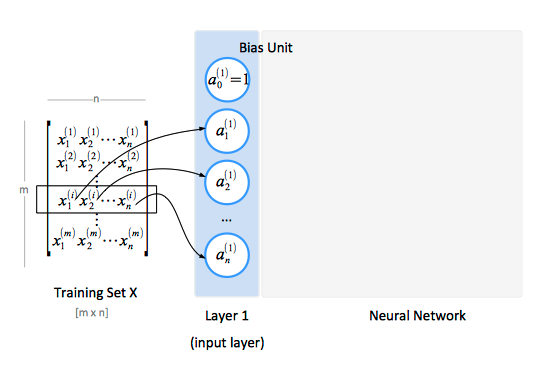
Input Layer

The input layer, conventionally named "layer 1", consists of input nodes. The input layer provides the training values during the training phase, and the input values during the classification phase. A training set contains a number of samples (m), and each sample has a number of features (n). The training set is conventionally represented as a matrix X.

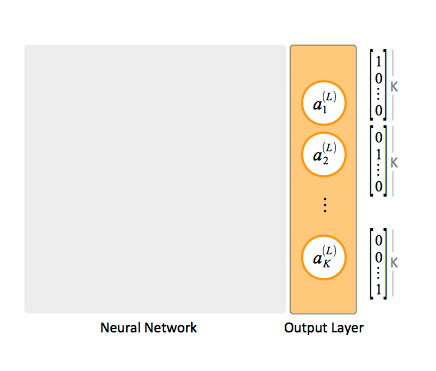
Output Layer

For multi-class classification, each y value of the training set is represented as a vector containing binary values. When an element of a specific class is matched, the corresponding unit in the output layer will product an "1" activation value, while all other units produce "0" activation values. The output layer has as many units as classes we are attempting to classify.

Forward Propagation

Forward propagation consists in calculating linear combinations of inputs and parameters for a layer, conventionally named z_i^(j), and applying sigmoid function to them.

If the layer j has p units, not counting the bias unit, and layer j + 1 has q units, not counting the bias unit, then the parameter matrix Θ^(j) controlling function mapping from layer j to layer j + 1 has q x (p + 1) elements. The "+1" comes from the addition of the bias node in layer j.

To compute the activation values of a layer j + 1, we calculate the weighted linear combination of the input values (or the activation values of the previous layer), conventionally named z_i^{(j + 1)}:

The vectorized implementation of forward propagation from layer j to layer j + 1 is averrable below:

To obtain the activation values of the output layer, we don't need to add the bias unit to the result vector.

Neural Network Training

The neural network training process consists of the following steps:

Weight Initialization

Weights should be initialized randomly to avoid the problem of symmetric ways.