Tree Concepts
Internal
Overview
A tree is a particular case of a graph.
Free Tree
A free tree is a connected, acyclic, undirected graph.
For an undirected graph G = (V, E), the following statements are equivalent:
- G is a free tree.
- Any two vertices in G are connected by a unique simple path.
- G is connected, but if any edge is removed from E, the resulting graph is disconnected.
- G is connected and │E│ = │V│ - 1.
- G is acyclic and │E│ = │V│ - 1.
- G is acyclic, but if any edge is added to E, the resulting graph contains a cycle.
Forest
If the undirected graph is acyclic, but disconnected, it is a forest.
Rooted Tree
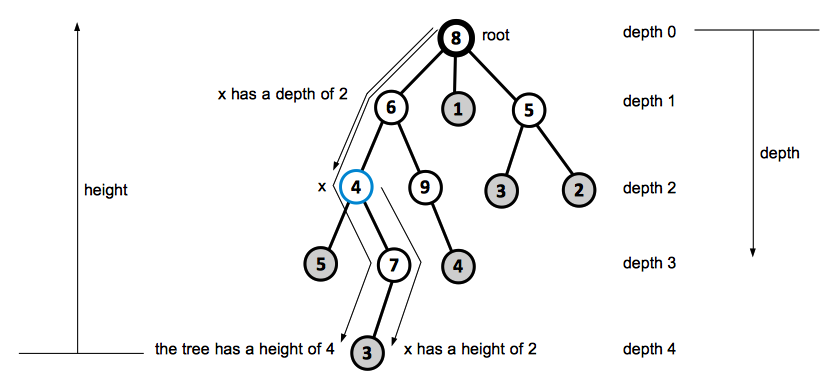
A rooted tree is a free tree in which one of the vertices is distinguished from the others.
We call the distinguished vertex the root of the tree.
We often refer to the vertex of a rooted tree as a node of the tree.
For a node x in a rooted tree, we call any node y on the simple path from root to x an ancestor of x. If y is an ancestor of x, then x is a descendant of y. Every node is both an ancestor and descendant of itself. If y is an ancestor of x and x ≠ y, then we call y a proper ancestor of x, and x is a proper descendant of y.
The subtree rooted at x is the tree induced by descendants of x, rooted at x.
If the last edge on the simple path from the root of the tree to a node x is (y, x), then y is the parent of x and x is the child of y. The root is the only node in the tree with no parent.
If two nodes have the same parent, they are siblings.
A node with no children is a leaf or an external node. A non-leaf node is an internal node.