Graph Concepts

Internal

• Graphs

Graph Definition

A graph is a pair-wise relationship among a set of objects. Mathematically, a graph G is a pair (V, E), where V is a finite set of vertices, called the vertex set of G, and E is a binary relation on G, called the edge set of G, which contains the graph's edges.

n and m Convention

In graph problems, the usual convention is to denote the number of vertices with n and the number of edges with m. In most, but not all, applications, m is Ω(n) and O(n²). Also see sparse graphs and dense graphs.

Vertices and Edges

Vertex (Node)

An elements of the vertex set V is called vertex (plural vertices). A vertex has zero or more edges associated with it. An alternate term for vertex, used sometimes in the graph theory literature, is node. We prefer to use the term "node" when we refer to the vertices of rooted trees. We use "vertex" as a more generic term that refers to graphs in general. Another alternate name is entity.

Vertex Adjacency

If (u, v) is an edge in a graph G = (V, E), we say that the vertex v is adjacent to vertex u. In other words, if two vertices have an edge connecting them, they are adjacent. For undirected graphs, the adjacency relation is symmetric: if vertex u is adjacent to vertex v, then automatically vertex v is adjacent to vertex u. This is not the case for directed graphs: u → v ≠ v → u.

Vertex Degree

The vertex degree is the count of edges incident on, from and to the vertex, depending on the type of the graph.

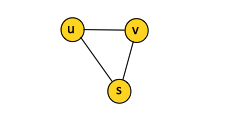
For undirected graphs, the vertex degree is the number of edges incident on the vertex, which is the same with the number of adjacent vertices. In the example below, the vertex v has degree 2.

For an undirected graphs, the following relationship holds true:

  ∑ degree(v) = 2m
  v

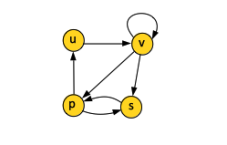
For directed graphs, we define the in-degree as the number of edges entering the vertex and the out-degree as the number of edges exiting the vertex. The degree of the vertex is the sum of in-degree and out-degree. In the example above, vertex v has an in-degree 2, out-degree 3 and degree 5.

Edge (Arc)

The element of the edge set E are called edges (also known as relationships or arcs). By convention, we use (u, v) notation for an edge, where u and v represent vertices in V. The order in which vertices are specified for an edge may be relevant. If the order in which the vertices are specified matters, then the graph is a directed graph. If the order in which the vertices are specified does not matter, then the graph is an undirected graph.

Parallel Arcs

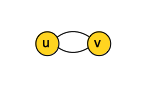
Two parallel arcs (or parallel edges) are two arcs that have the same vertices.

Graph Density

Sparse Graphs

A sparse graph is a graph for which │E│ is much smaller than │V│². Otherwise said, for a sparse graph m is O(n) or close to it.

Dense Graphs

A dense graph is a graph for which │E│ is close to │V│². Otherwise said, for a dense graph m is closer to O(n²).