Tree Concepts
Jump to navigation
Jump to search
Internal
Overview
A tree is a particular case of a graph.
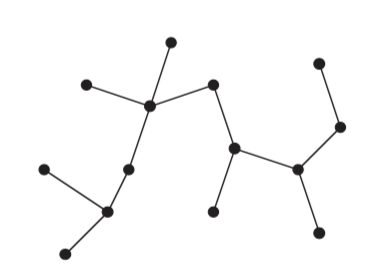
Free Tree
A free tree is a connected, acyclic, undirected graph.
For an undirected graph G = (V, E), the following statements are equivalent:
- G is a free tree.
- Any two vertices in G are connected by a unique simple path.
- G is connected, but if any edge is removed from E, the resulting graph is disconnected.
- G is connected and │E│ = │V│ - 1.
- G is acyclic and │E│ = │V│ - 1.
- G is acyclic, but if any edge is added to E, the resulting graph contains a cycle.
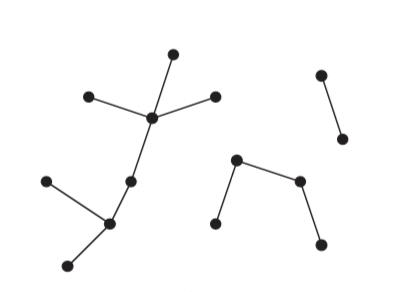
Forest
If the undirected graph is acyclic, but disconnected, it is a forest.