Tree Concepts
Internal
Overview
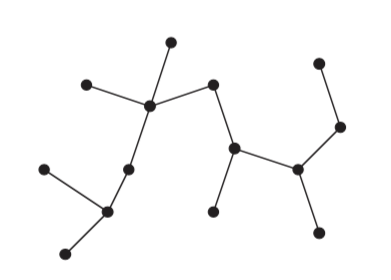
A tree is a particular case of a graph.
Free Tree
A free tree is a connected, acyclic, undirected graph.
For an undirected graph G = (V, E), the following statements are equivalent:
- G is a free tree.
- Any two vertices in G are connected by a unique simple path.
- G is connected, but if any edge is removed from E, the resulting graph is disconnected.
- G is connected and │E│ = │V│ - 1.
- G is acyclic and │E│ = │V│ - 1.
- G is acyclic, but if any edge is added to E, the resulting graph contains a cycle.
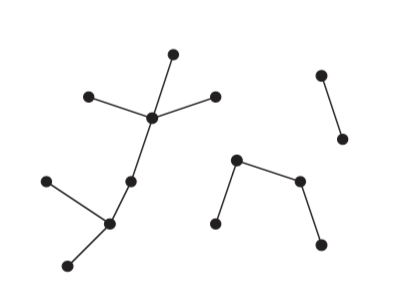
Forest
If the undirected graph is acyclic, but disconnected, it is a forest.
Rooted Tree
A rooted tree is a free tree in which one of the vertices is distinguished from the others.
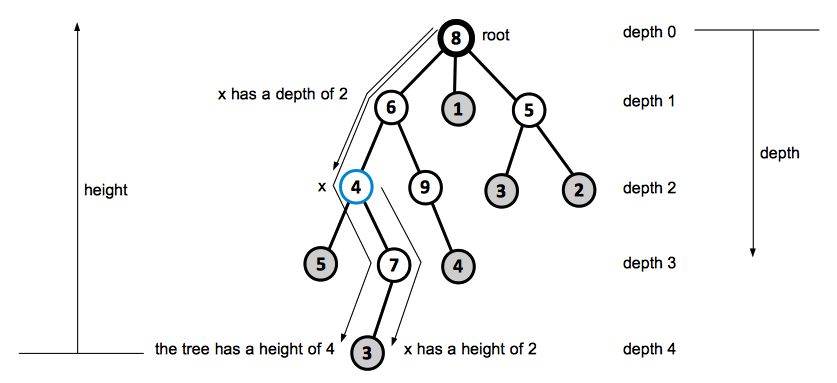
Root
We call the distinguished vertex the root of the tree.
Node
We often refer to the vertex of a rooted tree as a node of the tree.
Ancestors and Descendants
For a node x in a rooted tree, we call any node y on the simple path from root to x an ancestor of x. If y is an ancestor of x, then x is a descendant of y. Every node is both an ancestor and descendant of itself. If y is an ancestor of x and x ≠ y, then we call y a proper ancestor of x, and x is a proper descendant of y.
Subtree
The subtree rooted at x is the tree induced by descendants of x, rooted at x.
Parents, Children and Siblings
If the last edge on the simple path from the root of the tree to a node x is (y, x), then y is the parent of x and x is the child of y. The root is the only node in the tree with no parent. If two nodes have the same parent, they are siblings.
Leaf
A node with no children is a leaf or an external node. A non-leaf node is an internal node.
Degree
Note that the degree of a node depends on whether we consider the tree to be a rooted tree or a free tree.
In case of a free tree, the degree of a node is the degree of a vertex in an undirected graph, defined as the number of adjacent vertices.
For a rooted tree, the degree is the number of children - the parent of the node does not count toward its degree.
Depth and Height
The length of the simple path from the root to a node x, measured in the number of edges, is called the depth of the node x in the tree. The depth is always relative to the root.
A level of a tree consists of all nodes at the same depth.
The height of a node in a tree is the number of edges on the longest simple downward path from the node in question to a leaf.
The height of the tree is the height of its root. The height of the tree is also equal to the largest depth of any node in the tree.
The height is always relative to the lowest leaf.