Binary Codes
Internal
Overview
A binary code is a function that maps each character of an alphabet Σ to a binary string.
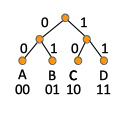
In general, any binary code can be expressed as a binary tree with the left child edges being labeled with 0s and right child edges being labeled with 1s, nodes being labeled with various symbols of the alphabet and the bits from the root down to the node labeled with the given symbol corresponding to the proposed encoding for that symbol.
Fixed Length Code
A fixed length binary code is a binary code that maps each character of the alphabet Σ to a fixed length code. Arbitrary characters have the same length representation in the binary code. ASCII is an example of a fixed length binary code. An example of fixed length code for the alphabet Σ = {A, B, C, D} is {00, 01, 10, 11}, where we use 2 bits per each character. If we think about binary codes as binary tree, the representation of this fixed length encoding as a binary tree is:
However, in case when some characters are more likely to appear than others, a schema that allocates shorter codes to characters that are likely to appear more frequently tends to encode information using fewer bits. This encoding schemas are called variable length codes.
Variable Length Code
A variable length binary code is a binary code that maps each character of the alphabet Σ to a variable length code, usually in relation to the frequency the character is used in certain patterns of communication. The more frequent characters are associated with shorter variable length codes, resulting in shorter encodings. Huffman codes are an example of variable length binary code.
A problem with variable length codes is that they may introduce ambiguity that makes decoding problematic. For example, in the case of the alphabet Σ = {A, B, C, D}, if we use the encoding {0, 1, 01, 10}, there is not enough information to decode 001. It could be decoded as AAB or as AC, because without further precautions, it is not clear when one symbol ends and another symbol begins. This problem is addressed by prefix-free codes.
Producing an efficient variable length code requires a priori domain knowledge, where we know the relative frequency of the alphabet symbols. For example, in genomics the usual frequency of A, C, G and Ts are known. In the case of encoding MP3s, we can take an intermediate version of the file after the analog-to-digital conversion is done and count the occurrences of each of the symbols.
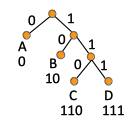
Prefix-Free Codes
Prefix-free codes solve the ambiguity of decoding variable length code-encoded content.
A prefix-free code is defined as follows: for every pair i,j of characters in the alphabet Σ, neither of the encodings f(i) and f(j) is a prefix of the other.
In the previous example, the {0, 1, 01, 10} encoding of the alphabet Σ = {A, B, C, D} is not prefix free, as A and C encodings have the same prefix, and also B and D. However, {0, 10, 110, 111} is a prefix free encoding. If we represent a prefix-free encoding as a binary tree, the tree nodes are associated with characters only for the leaves of the tree. The tree is not balanced.
The befit of thinking about prefix-code as trees is that the prefix-free condition shows up in a clean way in these trees, namely the prefix-free condition is the same as leaves being the only nodes that have character labels. No internal nodes are allowed to have a label in a prefix-free code. The code of a character is given by the bits along paths from root to the labeled node, and since all labeled nodes are leafs, no path of a node is the prefix of the other. For a node to have a code that is a prefix to other node's code is to be the ancestor of the other node in the tree, and since all nodes are leafs, no node is the ancestor of other node.