Tree Concepts

Internal

• Trees
• Data Structures
• Graphs

Overview

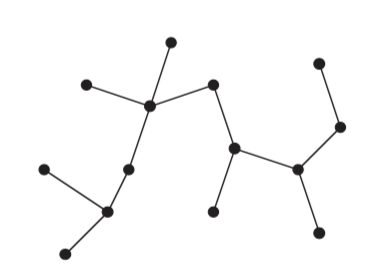
A tree is a particular case of a graph.

Free Tree

A free tree is a connected, acyclic, undirected graph.

For an undirected graph G = (V, E), the following statements are equivalent:

1. G is a free tree.
2. Any two vertices in G are connected by a unique simple path.
3. G is connected, but if any edge is removed from E, the resulting graph is disconnected.
4. G is connected and │E│ = │V│ - 1.
5. G is acyclic and │E│ = │V│ - 1.
6. G is acyclic, but if any edge is added to E, the resulting graph contains a cycle.

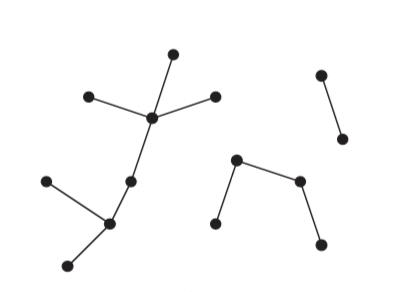
Forest

If the undirected graph is acyclic, but disconnected, it is a forest.

Rooted Tree

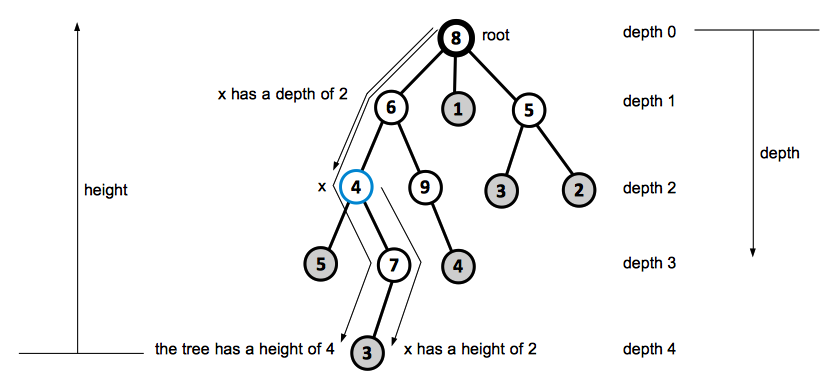
A rooted tree is a free tree in which one of the vertices is distinguished from the others.

Root

We call the distinguished vertex the root of the tree.

Node

We often refer to the vertex of a rooted tree as a node of the tree.

Ancestors and Descendants

For a node x in a rooted tree, we call any node y on the simple path from root to x an ancestor of x. If y is an ancestor of x, then x is a descendant of y. Every node is both an ancestor and descendant of itself. If y is an ancestor of x and x ≠ y, then we call y a proper ancestor of x, and x is a proper descendant of y.

Subtree

The subtree rooted at x is the tree induced by descendants of x, rooted at x.

Parents, Children and Siblings

If the last edge on the simple path from the root of the tree to a node x is (y, x), then y is the parent of x and x is the child of y. The root is the only node in the tree with no parent. If two nodes have the same parent, they are siblings.

Leaf

A node with no children is a leaf or an external node. A non-leaf node is an internal node.

Depth and Height

Depth

The length of the simple path from the root to a node x, measured in the number of edges, is called the depth of the node x in the tree. The depth is always relative to the root.

Level

A level of a tree consists of all nodes at the same depth.

Height

The height of a node in a tree is the number of edges on the longest simple downward path from the node in question to a leaf.

The height of the tree is the height of its root. The height of the tree is also equal to the largest depth of any node in the tree.

The height is always relative to the lowest leaf.

Degree

Note that the degree of a node depends on whether we consider the tree to be a rooted tree or a free tree.

In case of a free tree, the degree of a node is the degree of a vertex in an undirected graph, defined as the number of adjacent vertices.

For a rooted tree, the degree is the number of children. The parent of the node does not count toward its degree.

Ordered Tree

An ordered tree is a rooted tree in which the children of each node are ordered. If a node has k children, then there is a first child, a second child, and the k^th child. Also see Difference between Binary Trees and Ordered Trees.

Positional Tree

In a positional tree, the children of a node are labeled with distinct positive integers. The i^th child of a node is absent if no child is labeled with integer i.

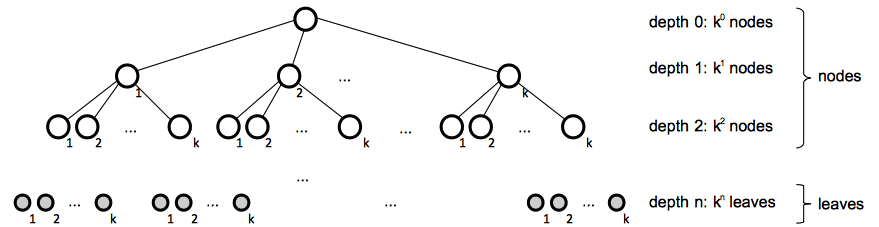
K-ary Tree

A k-ary tree is a positional tree in which for every node, all children with labels greater than k are absent.

A complete k-ary tree is a k-ary tree in which all leaves have the same depth and all internal nodes have degree k.

K-ary Tree Arithmetic

A complete k-ary tree of height h has k⁰ + k¹⁺ + ... + k^h-1 = (k^h - 1)/(k - 1) nodes and k^h leaves.

The height of a complete k-ary tree with n leaves is log_kn.

Types of K-ary Trees

B and B+ Trees

B and B+ Trees

Binary Tree

A binary tree is defined recursively as a structure defined on a finite set of nodes that either:

• contains no nodes
• is composed of three disjoint sets of nodes: a root node, a binary tree called its left subtree and a binary tree called its right subtree.

If the left subtree is not empty, its root is called the left child of the root of the entire tree. If the right subtree is not empty, its root is called the right child of the root of the entire tree.

A binary tree can also be defined as a k-ary tree with k=2.

Complete Binary Tree

A full binary tree, or a complete binary tree, is a binary tree where each node is either a leaf, or has a degree of exactly 2 - there are no degree-1 nodes.

As Complete as Possible

There is also the concept of a tree "as complete as possible", or "as balanced as possible", where the all the layers in the tree are complete, with exception of the highest layer, which may be incomplete. This property of binary trees is relevant when building heaps.

Difference between Binary Trees and Ordered Trees

A binary tree isn't simply an ordered tree with a degree of at most 2. In an ordered tree, there is no distinguishing a sole child as being either left or right. For a binary tree, the left or right position matters, so from this perspective, the concept of binary tree is stronger than the one of ordered tree. Binary trees can be implemented using ordered trees, if we maintain the position information necessary to a binary tree by replacing each missing child in the binary tree with a node having no children.

Binary Search Tree

A binary search tree is represented in memory using three pointers: left child, right child and the parent. More details on binary tree representation in memory are available here:

Binary Tree Representation in Memory

Binary Search Tree Property

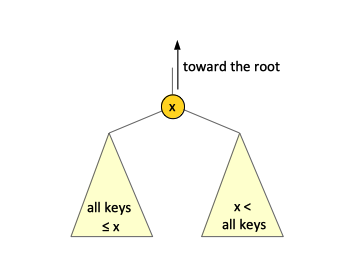
The fundamental property of the binary search tree, called the Binary Search Tree Property:

For every single node of a binary search tree, if the node has a key value, then all of the keys stored in the left subtree should be less than the node's key value and all of the keys stored in the right subtree should be bigger than the node's key value. This property holds not only at the root, but in every single node of the three.

Note that the Binary Search Tree Property is different from the Heap Property. Search tree are designed so we can search easily through them, unlike heaps that are designed to find the minimum (or maximum) easily.

TODO CLRS Page 286.

=Balances vs. Unbalanced Binary Search Trees

A binary search tree can be unbalanced or balanced. For the same set of key, the search tree can vary in height between log n and n, where n is the number of keys. Balanced trees are more useful for search because they yield better running times.

Balanced Binary Search Tree

Balanced Binary Search Trees

Red-Black Trees

Red-Black Tree

Radix Trees (Tries)

Radix Trees (Tries)

Heaps

Heaps

Tree Walking

Inorder

Inorder tree walk can be used to print a binary search tree node keys in sorted order.